【乐虎集团的官方网站
】<接上期——>
4.3 摩擦阻尼的影响
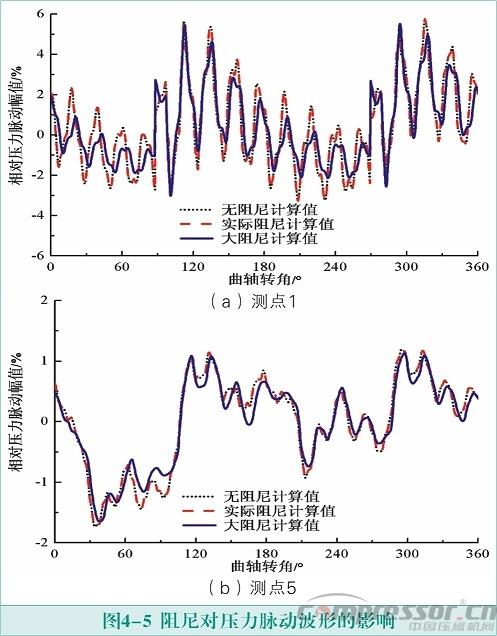
非定常方法等截面管流体动量方程(2-3)中摩擦系数 是一个可变值,可以由经验公式计算出,令 =0,则动量方程不再有阻尼项。为了分析阻尼的影响,分别对无阻尼 =0和有实际阻尼 ≠0的情况进行计算。结果表明有、无阻尼情况下,脉动幅值变化非常小。为排除摩擦系数计算值偏小的可能原因,将摩擦系数在实际计算的基础上增大1000倍,发现脉动幅值变化依然很小。如图3-2所示,给出了测点1和测点5在无阻尼、实际阻尼和阻尼增大1000倍三种情况计算波形的对比。测点1是非定常方法脉动幅值计算z*大的点,测点5是计算精度较高的点,因此选择这两个有代表性的测点观察阻尼对波形的影响。可以看出即使阻尼增大1000倍,压力脉动波形变化仍然很小。
如表4-3所示,无阻尼脉动幅值计算结果与实际阻尼计算值差别很小,即使将摩擦系数增大1000倍后的大阻尼情况,只有测点1、2、3脉动幅值才有明显下降,而测点4、5、6降幅很小。以上计算表明阻尼对脉动幅值几乎没有影响,当脉动幅值较大时,阻尼对压力脉动的抑制作用仍然很小。
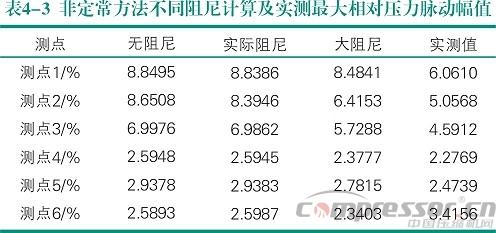
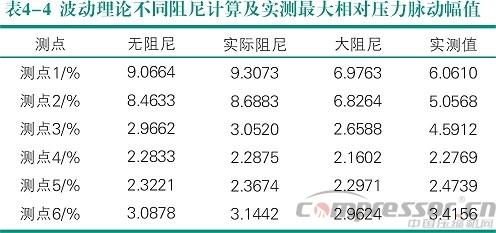
用波动理论分别对无阻尼、实际阻尼和大阻尼情况进行了计算。波动理论实际摩擦系数取非定常方法计算平均值0.005,大阻尼情况将摩擦系数增大了10倍。计算结果如表4-4所示。波动理论计算结果也表明无阻尼与实际阻尼幅值变化很小,大阻尼下脉动幅值测点1、2、3有显著降低,但测点4、5、6下降幅度很小。波动理论计算结果也表明摩擦阻尼对压力脉动幅值几乎没有抑制作用。
为了从根本上分析阻尼在脉动中的作用。有必要对方程本身作分析。下面重新给出有阻尼的动量方程:
式中: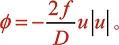
方程(4-1)是对控制体内流体运动建立的动量方程,其左端第一项表示气体的惯性。当控制体长度 越短,认为此越接近实际流动,方程建立的思想是用空间有限的距离推导出流体的一般运动规律。这种方程需要数值解法,根据有限差分法用离散的点描述连续问题的基本思想,这里用
越短,认为此越接近实际流动,方程建立的思想是用空间有限的距离推导出流体的一般运动规律。这种方程需要数值解法,根据有限差分法用离散的点描述连续问题的基本思想,这里用 近似
近似 ,
, 近似
近似 ,沿管道长度
,沿管道长度 的控制体近似长度为
的控制体近似长度为 的控制体,如图4-6所示。方程(4-1)就可以用差分法近似求解。
的控制体,如图4-6所示。方程(4-1)就可以用差分法近似求解。
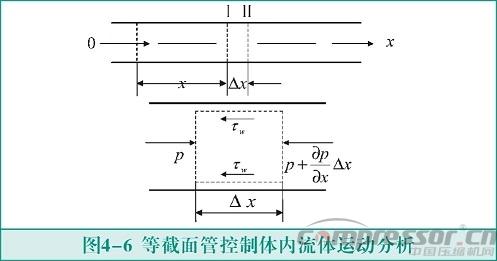
这里只对 长度的控制体,一个时间步
长度的控制体,一个时间步 进行计算定量分析。控制体内参数取实验参数,也是前面非定常方法计算的工况参数:控制体内平均压力为0.62MPa(绝对压力),声速为371.7 m·s-1,
进行计算定量分析。控制体内参数取实验参数,也是前面非定常方法计算的工况参数:控制体内平均压力为0.62MPa(绝对压力),声速为371.7 m·s-1, 取0.04m,假定管道平均流速为0,根据差分格式稳定条件
取0.04m,假定管道平均流速为0,根据差分格式稳定条件 ,时间步长为
,时间步长为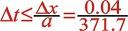 ≈0.000107s,为计算方便取
≈0.000107s,为计算方便取 =0.0001s,假定节点1、节点2是相邻的两个节点,它们的距离为
=0.0001s,假定节点1、节点2是相邻的两个节点,它们的距离为 。用
。用  、 代表节点1、2在
、 代表节点1、2在 时刻的速度,
时刻的速度,  代表节点1、2在
代表节点1、2在 时刻的速度,密度和压力表示法与此相同。则方程(4-1)在节点1、2处的局部差分形式为:
时刻的速度,密度和压力表示法与此相同。则方程(4-1)在节点1、2处的局部差分形式为: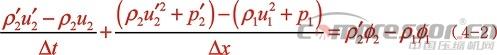
式中:
为计算方便假定 时刻
时刻 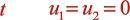 ,这种假设在实际中也是存在的:由于压力脉动,节点的瞬态速度有可能为0。于是化为:
,这种假设在实际中也是存在的:由于压力脉动,节点的瞬态速度有可能为0。于是化为: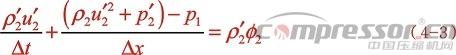
计算压力脉动幅值突然增大50%的情况:令节点1的压力为  =0.62MPa,由于压力增大50%,则0.0001s后节点2的压力变为
=0.62MPa,由于压力增大50%,则0.0001s后节点2的压力变为 =0.93MPa,下面分析这个瞬态过程方程(4-3)中密度和速度的变化。
=0.93MPa,下面分析这个瞬态过程方程(4-3)中密度和速度的变化。
假定这个过程为等熵过程,则 的密度可由等熵过程方程求得:
的密度可由等熵过程方程求得: 则 摩擦系数
则 摩擦系数 取经验值0.005。于是方程(4-3)中只有
取经验值0.005。于是方程(4-3)中只有 一个未知数,可以对其求解:
一个未知数,可以对其求解:

上式中,压力和密度都增大,为保持方程成立, 必然是负值,则上式可化为:
必然是负值,则上式可化为:

上式中92700  是气体惯性项,-1.43 是气体与管道壁面摩擦阻力项。可见方程(4-6)中只有气体惯性力和摩擦力抑制节点2压力的增大。解出
是气体惯性项,-1.43 是气体与管道壁面摩擦阻力项。可见方程(4-6)中只有气体惯性力和摩擦力抑制节点2压力的增大。解出 就可以知道气体惯性力和摩擦阻尼力对抑制压力脉动作用的大小。对方程(4-6)合并二次项,z*终化为:
就可以知道气体惯性力和摩擦阻尼力对抑制压力脉动作用的大小。对方程(4-6)合并二次项,z*终化为:
上式是一个标准抛物线方程,有实根,解得:

以上算出了两个根,实际只能是其中一个根。当压力脉动幅值减小时,脉动速度也应该减小,可以计算出方程(4-7)的两个根,一个减小,另一个增大,减小的那个根才是符合实际的解。据此判断出方程(4-7)的实际解为 。则方程(4-6)中气体惯性力为:
。则方程(4-6)中气体惯性力为:
方程(4-6)中摩擦阻尼力为:
可以算出气体惯性力是摩擦阻尼力的533倍。 越大,摩擦力增加更快,但并不是无限增加,因为等截面管气流流速z*高只能到音速。当
越大,摩擦力增加更快,但并不是无限增加,因为等截面管气流流速z*高只能到音速。当 等于当地音速371.7 m·s-1时,可以算出气体惯性项仍高达摩擦阻尼项的174倍。以上计算表明气体惯性力是平衡压力脉动z*主要的因素,气体与管道壁面摩擦作用对压力脉动的抑制很小,即使将摩擦系数增大数十倍,相比气体惯性力仍然很小。
等于当地音速371.7 m·s-1时,可以算出气体惯性项仍高达摩擦阻尼项的174倍。以上计算表明气体惯性力是平衡压力脉动z*主要的因素,气体与管道壁面摩擦作用对压力脉动的抑制很小,即使将摩擦系数增大数十倍,相比气体惯性力仍然很小。
以上分析发现阻尼对压力脉动幅值影响很小,有助于认识忽略了阻尼因素的波动理论在大脉动情况下计算不准确的原因,下面进行分析。
波动理论的无阻尼运动方程为:
上式中将压力、速度、密度都看作平均参数和脉动参数的叠加,即  ,将其代入(4-8)忽略二阶项,作线性化处理后得:
,将其代入(4-8)忽略二阶项,作线性化处理后得:

式中:
 ——管道气流平均流速/m·s-1;
——管道气流平均流速/m·s-1;
 ——气流平均压力下的密度/ kg·m-3。
——气流平均压力下的密度/ kg·m-3。
从上式可以看出气流密度始终是常数,不随压力波动而变化。同样对(4-9)作局部差分得:
上式各参数取值与前面计算分析相同,压力脉动幅值仍为50%,管道平均流速取 ,令
,令
则(4-10)化为:

求得 =103.7 ,可见脉动速度远远高出平均流速,所以速度项不能做线性化假设,令式(4-10)中
=103.7 ,可见脉动速度远远高出平均流速,所以速度项不能做线性化假设,令式(4-10)中 ,则(4-9)化为:
,则(4-9)化为:

对上式作局部差分处理得:


上式没有实根。可以预测随着脉动幅值降低,式(4-13)中的常数项减小,会有实数解。
以上分析表明波动理论将密度视为常数,导致大脉动情况下运动方程没有实数解。数值方法求解时,随着计算的进行会出现密度为负值的现象,当密度为负时,式(4-13)有实数解,但已违背了基本自然规律。但这种情况下波动理论仍能求解,因为波动理论求出的脉动参数是复数形式,计算出(4-13)的复数脉动速度是非定常方法计算脉动速度的1.75倍,于是可算出波动理论气体惯性力是非定常方法计算值的0.6倍。
综合以上分析,可以得出结论:等截面管内气流与管道壁面的摩擦力对压力脉动幅值的影响很小,抑制压力脉动的z*主要因素是气流惯性。
4.4 局部阻力的影响
同时也注意到管道AB上的测点1、2、3非定常方法和波动理论计算的脉动幅值均高于实测值。这段管路的容积值已经与实测管路容积相等,按照之前气体惯性是平衡压力脉动的主要因素,两种方法都出现了计算值高于实测值的情况,说明控制方程中忽略了某些因素。回顾管道AB是作了简化处理,气缸排气口到连接法兰的流道结构复杂,计算过程中将其简化为等截面的直管,等截面直管只有气体与管道壁面摩擦导致的沿程阻力损失,这个损失非常小,前面所做阻尼分析指出这种损失对脉动幅值影响也很小。复杂流道流通面积发生突变引起比沿程阻力损失大很多的局部阻力损失,但控制方程(2-10)中并没有包含这种由于截面变化引起的阻力和能量损失。因此准确预测复杂流道的压力脉动需要在控制方程中加入截面变化因素。修正方程组(2-10)为:

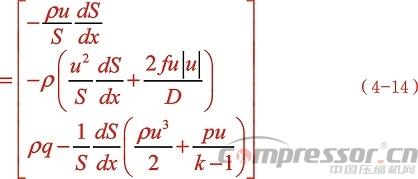
管道AB内径为0.12m,假设在 =0.04m的距离上内径缩小一半变为0.06m,则加入截面变化项后,式(4-5)变为:
=0.04m的距离上内径缩小一半变为0.06m,则加入截面变化项后,式(4-5)变为:

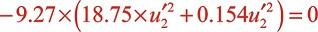
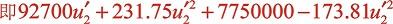

上式z*终化为: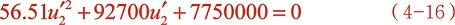
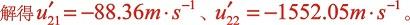
很明显 远大于音速,实际不可能为此解。下面分析各项的大小:
远大于音速,实际不可能为此解。下面分析各项的大小:
惯性力: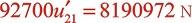
突变截面局部阻力: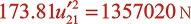
摩擦力: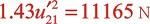
气体惯性力是摩擦力的734倍,但仅是突变截面局部阻力的6倍,突变截面局部阻力是摩擦阻尼力的122倍。说明突变截面产生的局部阻力在平衡压力脉动中起了很大作用。在有变截面的管道中,若动量方程中没有此项,压力的波动全靠气体惯性平衡,导致气体瞬态密度和速度出现较大的振荡,不容易收敛,极限情况会出现密度为负值,导致计算中断。即使获得收敛解,但计算脉动幅值偏大,压力脉动波形出现很多振荡剧烈的高频波。测点1、2、3计算波形证明了这一点,气缸排气口至缓冲罐进口的管段ABz*靠近脉动激发源,非稳态流动更剧烈,受阀片运动等因素影响,脉动幅值更高、高频波比下游管路更多,计算时若没有截面变化损失项的平衡,仅靠气体惯性衰减的还不够,z*终导致高频波远多于实测值,而且脉动幅值偏高。
5、结论与展望
5.1 结论
本文以一维非定常可压缩流动理论为基础,建立了描述nianxiangyuan
管道内压力脉动与非稳态流动的数学模型,搭建了nianxiangyuan
管道气流脉动研究实验台,在二级排气管路布置了多个动态压力测点,测量了管路不同位置处的压力脉动,通过对比实验值和计算结果,得出以下主要结论:
1)一维非定常可压缩流动数学模型能够在较长的等截面管道上较准确的预测出压力脉动幅值,而且压力脉动波形与实测波形也吻合的良好。由于是一维网格,对形状较复杂的流道须作简化处理,作简化处理的局部管路,计算脉动幅值与实测值偏差较大,但离开一段距离后的其它处管路计算幅值仍然与实测值较接近;实验台缓冲罐之前管路计算时作了简化处理,脉动幅值z*大相差3.33%,缓冲罐之后的管路未作简化处理,计算压力脉动幅值与实测值z*大相差0.82%。
2)用有限差分法求解描述气流脉动的双曲型控制方程组时,对网格划分有特殊要求,网格稀疏将使压力波的高频成分在数值计算过程中被衰减,z*终得到的波形光滑。为保证一定频率范围的压力波不被衰减,网格长度必须满足波长比条件,波长与网格长度的比值应大于40,才能保证该频率的波无衰减的计算出。
3)阻尼对压力脉动的抑制作用很小,有阻尼与无阻尼的计算结果基本一致。抑制压力脉动z*主要的因素是气体本身的惯性,动量方程中气体惯性力比摩擦阻尼力高出几个数量级,实验管路相对压力脉动幅值为50%时,气体惯性力是摩擦阻尼力的533倍。波动理论因将密度视为常数,惯性项小于非定常方法计算值,导致计算脉动参数偏大。实验管路相对脉动幅值为50%时,波动理论计算惯性力是非定常方法计算值的0.6倍,而脉动速度是非定常方法计算值的1.75倍。
4)管道系统内局部阻力远大于气体与管道壁面的沿程摩擦阻力,沿实验管道长度0.04m,管道内径由0.12m缩小一半,所产生的局部阻力是沿程摩擦阻力的122倍。因此在变截面处,除惯性力外,局部阻力也是抑制压力脉动的一个重要因素。它的存在降低了瞬态密度和速度的振荡,使计算更容易收敛。
5.2 未来工作展望
实际管道系统往往结构复杂,气流脉动更不易分析,数学模型上肯定还有未考虑到的因素,对数值求解方法的计算特性掌握的还不够充分。综合本文对一维非定常流动方程数值计算和定量分析阻尼、气体惯性力所做工作。对今后工作展望如下:
1)本文使用有限差分的数值解法,近年来有限元技术飞速发展,气流脉动的双曲型控制方程组用有限体积法求解,更容易得到收敛解,也适合计算复杂管路。将来有必要探讨使用此数值方法计算复杂管道内的气流脉动。
2)实际管路气体通流截面往往有变化,如孔板、阀门、气缸吸、排气口等处流道截面变化很大,变截面管比等截面管的控制方程更复杂,数值求解难度更大,处理好这个问题,有助于提高变截面处的计算精度,这对孔板、阀门和节流元件的气流脉动研究很有意义。
由于能力和时间有限,本文必然存在不完美、不成熟的地方,还有很多工作没能作进一步的深入讨论,真诚的希望学界前辈和同仁们能给予批评指正。本人也将更加努力地在气流脉动的研究工作中多做些事情。
(参考文献略)(全文完)
来源:■文/西安交通大学 王中振
【乐虎集团的官方网站 】<接上期——>
4.3 摩擦阻尼的影响
非定常方法等截面管流体动量方程(2-3)中摩擦系数 是一个可变值,可以由经验公式计算出,令 =0,则动量方程不再有阻尼项。为了分析阻尼的影响,分别对无阻尼 =0和有实际阻尼 ≠0的情况进行计算。结果表明有、无阻尼情况下,脉动幅值变化非常小。为排除摩擦系数计算值偏小的可能原因,将摩擦系数在实际计算的基础上增大1000倍,发现脉动幅值变化依然很小。如图3-2所示,给出了测点1和测点5在无阻尼、实际阻尼和阻尼增大1000倍三种情况计算波形的对比。测点1是非定常方法脉动幅值计算z*大的点,测点5是计算精度较高的点,因此选择这两个有代表性的测点观察阻尼对波形的影响。可以看出即使阻尼增大1000倍,压力脉动波形变化仍然很小。
如表4-3所示,无阻尼脉动幅值计算结果与实际阻尼计算值差别很小,即使将摩擦系数增大1000倍后的大阻尼情况,只有测点1、2、3脉动幅值才有明显下降,而测点4、5、6降幅很小。以上计算表明阻尼对脉动幅值几乎没有影响,当脉动幅值较大时,阻尼对压力脉动的抑制作用仍然很小。


用波动理论分别对无阻尼、实际阻尼和大阻尼情况进行了计算。波动理论实际摩擦系数取非定常方法计算平均值0.005,大阻尼情况将摩擦系数增大了10倍。计算结果如表4-4所示。波动理论计算结果也表明无阻尼与实际阻尼幅值变化很小,大阻尼下脉动幅值测点1、2、3有显著降低,但测点4、5、6下降幅度很小。波动理论计算结果也表明摩擦阻尼对压力脉动幅值几乎没有抑制作用。

为了从根本上分析阻尼在脉动中的作用。有必要对方程本身作分析。下面重新给出有阻尼的动量方程:
式中: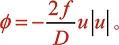
方程(4-1)是对控制体内流体运动建立的动量方程,其左端第一项表示气体的惯性。当控制体长度 越短,认为此越接近实际流动,方程建立的思想是用空间有限的距离推导出流体的一般运动规律。这种方程需要数值解法,根据有限差分法用离散的点描述连续问题的基本思想,这里用
越短,认为此越接近实际流动,方程建立的思想是用空间有限的距离推导出流体的一般运动规律。这种方程需要数值解法,根据有限差分法用离散的点描述连续问题的基本思想,这里用 近似
近似 ,
, 近似
近似 ,沿管道长度
,沿管道长度 的控制体近似长度为
的控制体近似长度为 的控制体,如图4-6所示。方程(4-1)就可以用差分法近似求解。
的控制体,如图4-6所示。方程(4-1)就可以用差分法近似求解。

这里只对 长度的控制体,一个时间步
长度的控制体,一个时间步 进行计算定量分析。控制体内参数取实验参数,也是前面非定常方法计算的工况参数:控制体内平均压力为0.62MPa(绝对压力),声速为371.7 m·s-1,
进行计算定量分析。控制体内参数取实验参数,也是前面非定常方法计算的工况参数:控制体内平均压力为0.62MPa(绝对压力),声速为371.7 m·s-1, 取0.04m,假定管道平均流速为0,根据差分格式稳定条件
取0.04m,假定管道平均流速为0,根据差分格式稳定条件 ,时间步长为
,时间步长为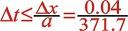 ≈0.000107s,为计算方便取
≈0.000107s,为计算方便取 =0.0001s,假定节点1、节点2是相邻的两个节点,它们的距离为
=0.0001s,假定节点1、节点2是相邻的两个节点,它们的距离为 。用
。用  、 代表节点1、2在
、 代表节点1、2在 时刻的速度,
时刻的速度,  代表节点1、2在
代表节点1、2在 时刻的速度,密度和压力表示法与此相同。则方程(4-1)在节点1、2处的局部差分形式为:
时刻的速度,密度和压力表示法与此相同。则方程(4-1)在节点1、2处的局部差分形式为: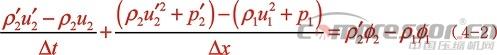
式中:
为计算方便假定 时刻
时刻 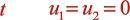 ,这种假设在实际中也是存在的:由于压力脉动,节点的瞬态速度有可能为0。于是化为:
,这种假设在实际中也是存在的:由于压力脉动,节点的瞬态速度有可能为0。于是化为: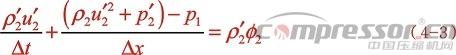
计算压力脉动幅值突然增大50%的情况:令节点1的压力为  =0.62MPa,由于压力增大50%,则0.0001s后节点2的压力变为
=0.62MPa,由于压力增大50%,则0.0001s后节点2的压力变为 =0.93MPa,下面分析这个瞬态过程方程(4-3)中密度和速度的变化。
=0.93MPa,下面分析这个瞬态过程方程(4-3)中密度和速度的变化。
假定这个过程为等熵过程,则 的密度可由等熵过程方程求得:
的密度可由等熵过程方程求得: 则 摩擦系数
则 摩擦系数 取经验值0.005。于是方程(4-3)中只有
取经验值0.005。于是方程(4-3)中只有 一个未知数,可以对其求解:
一个未知数,可以对其求解:

上式中,压力和密度都增大,为保持方程成立, 必然是负值,则上式可化为:
必然是负值,则上式可化为:

上式中92700  是气体惯性项,-1.43 是气体与管道壁面摩擦阻力项。可见方程(4-6)中只有气体惯性力和摩擦力抑制节点2压力的增大。解出
是气体惯性项,-1.43 是气体与管道壁面摩擦阻力项。可见方程(4-6)中只有气体惯性力和摩擦力抑制节点2压力的增大。解出 就可以知道气体惯性力和摩擦阻尼力对抑制压力脉动作用的大小。对方程(4-6)合并二次项,z*终化为:
就可以知道气体惯性力和摩擦阻尼力对抑制压力脉动作用的大小。对方程(4-6)合并二次项,z*终化为:
上式是一个标准抛物线方程,有实根,解得:

以上算出了两个根,实际只能是其中一个根。当压力脉动幅值减小时,脉动速度也应该减小,可以计算出方程(4-7)的两个根,一个减小,另一个增大,减小的那个根才是符合实际的解。据此判断出方程(4-7)的实际解为 。则方程(4-6)中气体惯性力为:
。则方程(4-6)中气体惯性力为:
方程(4-6)中摩擦阻尼力为:
可以算出气体惯性力是摩擦阻尼力的533倍。 越大,摩擦力增加更快,但并不是无限增加,因为等截面管气流流速z*高只能到音速。当
越大,摩擦力增加更快,但并不是无限增加,因为等截面管气流流速z*高只能到音速。当 等于当地音速371.7 m·s-1时,可以算出气体惯性项仍高达摩擦阻尼项的174倍。以上计算表明气体惯性力是平衡压力脉动z*主要的因素,气体与管道壁面摩擦作用对压力脉动的抑制很小,即使将摩擦系数增大数十倍,相比气体惯性力仍然很小。
等于当地音速371.7 m·s-1时,可以算出气体惯性项仍高达摩擦阻尼项的174倍。以上计算表明气体惯性力是平衡压力脉动z*主要的因素,气体与管道壁面摩擦作用对压力脉动的抑制很小,即使将摩擦系数增大数十倍,相比气体惯性力仍然很小。
以上分析发现阻尼对压力脉动幅值影响很小,有助于认识忽略了阻尼因素的波动理论在大脉动情况下计算不准确的原因,下面进行分析。
波动理论的无阻尼运动方程为:
上式中将压力、速度、密度都看作平均参数和脉动参数的叠加,即  ,将其代入(4-8)忽略二阶项,作线性化处理后得:
,将其代入(4-8)忽略二阶项,作线性化处理后得:

式中:
 ——管道气流平均流速/m·s-1;
——管道气流平均流速/m·s-1;
 ——气流平均压力下的密度/ kg·m-3。
——气流平均压力下的密度/ kg·m-3。
从上式可以看出气流密度始终是常数,不随压力波动而变化。同样对(4-9)作局部差分得:
上式各参数取值与前面计算分析相同,压力脉动幅值仍为50%,管道平均流速取 ,令
,令
则(4-10)化为:

求得 =103.7 ,可见脉动速度远远高出平均流速,所以速度项不能做线性化假设,令式(4-10)中
=103.7 ,可见脉动速度远远高出平均流速,所以速度项不能做线性化假设,令式(4-10)中 ,则(4-9)化为:
,则(4-9)化为:

对上式作局部差分处理得:


上式没有实根。可以预测随着脉动幅值降低,式(4-13)中的常数项减小,会有实数解。
以上分析表明波动理论将密度视为常数,导致大脉动情况下运动方程没有实数解。数值方法求解时,随着计算的进行会出现密度为负值的现象,当密度为负时,式(4-13)有实数解,但已违背了基本自然规律。但这种情况下波动理论仍能求解,因为波动理论求出的脉动参数是复数形式,计算出(4-13)的复数脉动速度是非定常方法计算脉动速度的1.75倍,于是可算出波动理论气体惯性力是非定常方法计算值的0.6倍。
综合以上分析,可以得出结论:等截面管内气流与管道壁面的摩擦力对压力脉动幅值的影响很小,抑制压力脉动的z*主要因素是气流惯性。
4.4 局部阻力的影响
同时也注意到管道AB上的测点1、2、3非定常方法和波动理论计算的脉动幅值均高于实测值。这段管路的容积值已经与实测管路容积相等,按照之前气体惯性是平衡压力脉动的主要因素,两种方法都出现了计算值高于实测值的情况,说明控制方程中忽略了某些因素。回顾管道AB是作了简化处理,气缸排气口到连接法兰的流道结构复杂,计算过程中将其简化为等截面的直管,等截面直管只有气体与管道壁面摩擦导致的沿程阻力损失,这个损失非常小,前面所做阻尼分析指出这种损失对脉动幅值影响也很小。复杂流道流通面积发生突变引起比沿程阻力损失大很多的局部阻力损失,但控制方程(2-10)中并没有包含这种由于截面变化引起的阻力和能量损失。因此准确预测复杂流道的压力脉动需要在控制方程中加入截面变化因素。修正方程组(2-10)为:

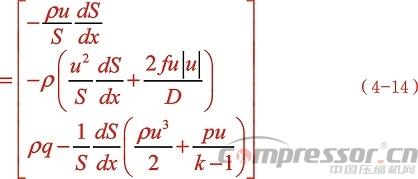
管道AB内径为0.12m,假设在 =0.04m的距离上内径缩小一半变为0.06m,则加入截面变化项后,式(4-5)变为:
=0.04m的距离上内径缩小一半变为0.06m,则加入截面变化项后,式(4-5)变为:

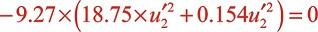
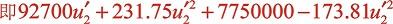

上式z*终化为: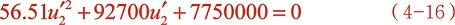
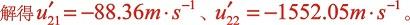
很明显 远大于音速,实际不可能为此解。下面分析各项的大小:
远大于音速,实际不可能为此解。下面分析各项的大小:
惯性力: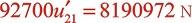
突变截面局部阻力: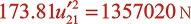
摩擦力: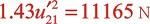
气体惯性力是摩擦力的734倍,但仅是突变截面局部阻力的6倍,突变截面局部阻力是摩擦阻尼力的122倍。说明突变截面产生的局部阻力在平衡压力脉动中起了很大作用。在有变截面的管道中,若动量方程中没有此项,压力的波动全靠气体惯性平衡,导致气体瞬态密度和速度出现较大的振荡,不容易收敛,极限情况会出现密度为负值,导致计算中断。即使获得收敛解,但计算脉动幅值偏大,压力脉动波形出现很多振荡剧烈的高频波。测点1、2、3计算波形证明了这一点,气缸排气口至缓冲罐进口的管段ABz*靠近脉动激发源,非稳态流动更剧烈,受阀片运动等因素影响,脉动幅值更高、高频波比下游管路更多,计算时若没有截面变化损失项的平衡,仅靠气体惯性衰减的还不够,z*终导致高频波远多于实测值,而且脉动幅值偏高。
5、结论与展望
5.1 结论
本文以一维非定常可压缩流动理论为基础,建立了描述nianxiangyuan
管道内压力脉动与非稳态流动的数学模型,搭建了nianxiangyuan
管道气流脉动研究实验台,在二级排气管路布置了多个动态压力测点,测量了管路不同位置处的压力脉动,通过对比实验值和计算结果,得出以下主要结论:
1)一维非定常可压缩流动数学模型能够在较长的等截面管道上较准确的预测出压力脉动幅值,而且压力脉动波形与实测波形也吻合的良好。由于是一维网格,对形状较复杂的流道须作简化处理,作简化处理的局部管路,计算脉动幅值与实测值偏差较大,但离开一段距离后的其它处管路计算幅值仍然与实测值较接近;实验台缓冲罐之前管路计算时作了简化处理,脉动幅值z*大相差3.33%,缓冲罐之后的管路未作简化处理,计算压力脉动幅值与实测值z*大相差0.82%。
2)用有限差分法求解描述气流脉动的双曲型控制方程组时,对网格划分有特殊要求,网格稀疏将使压力波的高频成分在数值计算过程中被衰减,z*终得到的波形光滑。为保证一定频率范围的压力波不被衰减,网格长度必须满足波长比条件,波长与网格长度的比值应大于40,才能保证该频率的波无衰减的计算出。
3)阻尼对压力脉动的抑制作用很小,有阻尼与无阻尼的计算结果基本一致。抑制压力脉动z*主要的因素是气体本身的惯性,动量方程中气体惯性力比摩擦阻尼力高出几个数量级,实验管路相对压力脉动幅值为50%时,气体惯性力是摩擦阻尼力的533倍。波动理论因将密度视为常数,惯性项小于非定常方法计算值,导致计算脉动参数偏大。实验管路相对脉动幅值为50%时,波动理论计算惯性力是非定常方法计算值的0.6倍,而脉动速度是非定常方法计算值的1.75倍。
4)管道系统内局部阻力远大于气体与管道壁面的沿程摩擦阻力,沿实验管道长度0.04m,管道内径由0.12m缩小一半,所产生的局部阻力是沿程摩擦阻力的122倍。因此在变截面处,除惯性力外,局部阻力也是抑制压力脉动的一个重要因素。它的存在降低了瞬态密度和速度的振荡,使计算更容易收敛。
5.2 未来工作展望
实际管道系统往往结构复杂,气流脉动更不易分析,数学模型上肯定还有未考虑到的因素,对数值求解方法的计算特性掌握的还不够充分。综合本文对一维非定常流动方程数值计算和定量分析阻尼、气体惯性力所做工作。对今后工作展望如下:
1)本文使用有限差分的数值解法,近年来有限元技术飞速发展,气流脉动的双曲型控制方程组用有限体积法求解,更容易得到收敛解,也适合计算复杂管路。将来有必要探讨使用此数值方法计算复杂管道内的气流脉动。
2)实际管路气体通流截面往往有变化,如孔板、阀门、气缸吸、排气口等处流道截面变化很大,变截面管比等截面管的控制方程更复杂,数值求解难度更大,处理好这个问题,有助于提高变截面处的计算精度,这对孔板、阀门和节流元件的气流脉动研究很有意义。
由于能力和时间有限,本文必然存在不完美、不成熟的地方,还有很多工作没能作进一步的深入讨论,真诚的希望学界前辈和同仁们能给予批评指正。本人也将更加努力地在气流脉动的研究工作中多做些事情。
(参考文献略)(全文完)
来源:■文/西安交通大学 王中振




网友评论
条评论
最新评论