【乐虎集团的官方网站
】某公司因为使用需要，接到任务要求开发一款转速n=1470r/mim，z*大活塞力P=160kN,4M型基础件。这对高转速、4M型的曲轴提出更高的精度要求。
相关人员分析研究后拟利用SolidWorks进行曲轴动平衡仿真，使曲轴达到国际标准ISO1940规定的平衡精度，并选取曲轴精度等级G6.3，依据动平衡原理（要求惯性力和惯性力矩都达到平衡），设计出基于SolidWorks的4M16曲轴动平衡仿真分析报告，并具体提出几种分析方法，以供参考施行研究。
方法一：Simulation有限元分析法
a)夹具：在曲轴两轴承端设置固定铰链，如图1所示。
b) 外部载荷：在旋转轴上添加旋转速度n=1470r/min，方向顺时针（从电机端往曲轴方向看去）如图2所示。
c) 网格化：对曲轴进行网格化，如图3所示。
d)运行并显示结果：如图4所示。
图中显示两端轴承受力情况，得出的合力即为旋转不平衡力F1=221.09N。
方法二：Motion运动分析法
a)新建运动算例，将曲轴两端设好的点分别与机身旋转轴（Z轴）重合。
b)设置旋转马达，转速n=1470r/min，方向顺时针，如图5所示。
c)添加重力：将Y轴正向设为重力方向（因为研究水平轴X方向受力，可以不设置重力），如图6所示。
d)点击计算按钮，输出两端支反力作用曲线图，如图7所示。
e)将左右两侧支反力进行矢量叠加，获得的曲线图如图8所示。
这是一条类正余弦曲线，其极值F2=221N（在水平方向0°和180°）。
方法三：传统计算法
a)原理：具有一定转速的转子，由于材料组织不均性、零件外形误差、装配误差以及结构形状局部不对称性（如键槽）等原因，使通过转子重心的主惯性轴与旋转轴线不重合，因而旋转时，转子产生不平衡离心力，其值如下式所示:
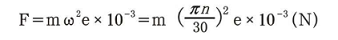
式中：m为转子的重量（kg）；ω为转子角速度（rad/s）；n为转子速度（r/min）；e为转子重心对旋转轴线的偏移，即偏心距（mm）。
b)由曲轴的质量属性可知曲轴质量，重心位置，如图9所示。
c)该曲轴旋转不平衡惯性力
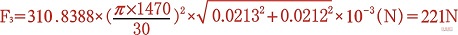
结论
从上述三种方法可知F1=F2=F3=221N，即无论使用Simulation有限元分析法还是Motion运动分析法，其结果与传统计算法得出的结果一致。
确定z*大往复质量Mp
已知电机转速n=1470r/mim，取综合活塞力
P=156kN，λ=0.1724，行程S=2r=2×63.5=127mm，则往复z*大质量Mpmax=P/[rω2（1+λ）]=88.4kg
取往复质量Mp=85kg[相对运动两列的往复运动重量误差，不得大于1磅（0.4536 kg）]
整机进行Motion运动仿真
将连杆、曲轴、活塞及活塞杆等运动件进行装配，在此装配体中进行Motion运动仿真（具体步骤见方法二），得出轴承两端受力曲线图，如图10所示。
从图中可知，左侧受力在±1.82×104 N成正余弦波动，右侧受力在±1.84×104 N成正余弦波动，该力组成的力矩是机组震动的根源。这种周期性变化的支反力是由于一阶惯性力矩不平衡引起的，必须予以降低甚至消除。
4M16曲轴连杆机构受力分析
1、气体力与摩擦力（旋转摩擦力和往复摩擦力）属于内力，它们均在机器内部相互抵消掉。
2、往复惯性力和旋转惯性力属于外力，它们在机器内部若不能平衡掉，那么它们会通过主轴承和机体传递至机器外部来。因为其数值大小和方向随着曲柄转角周期变化，会引起机器的振动和噪声，缩短轴承使用寿命。
3、往复惯性力：往复惯性力的大小由往复质量ms与其加速度a大小决定的，方向同加速度a方向，其表达式为I=msa=msω2r（cosθ+λcos2θ）
4、旋转惯性力：是由曲柄销质量mr沿着旋转轴旋转引起的，方向始终沿着曲柄销半径向外, 其表达式为Ir=mrω2r
5、4M16曲轴连杆机构简图如图11所示：第1列所处位置设为曲柄转角为0，b为相邻列间距，L为两端平衡重距离，δ为1、3列气缸中心线夹角等于90°，λ为1、2列气缸中心线夹角等于180°，其惯性力与惯性力矩如表1所示。
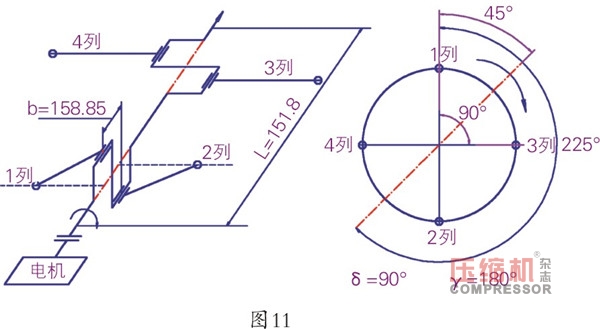
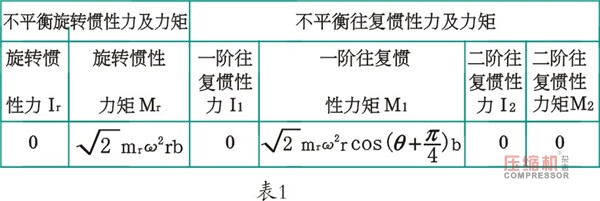
从表1中知旋转惯性力Ir、一阶往复惯性力I1、二阶往复惯性力I2、二阶往复惯性力矩M2均等于零；旋转惯性力矩Mr可在曲柄销对侧加平衡重来平衡（本文曲轴的Mr已配平衡，过程不再赘述）；一阶往复惯性力矩
，其极值在曲柄转角45°和225°方向上，故在其反方向225°和45°方向上加配重块进行平衡。一般在曲轴两端，因为此时力臂z*大，则配置块的质量z*轻，对曲轴平衡性能更有利。
6、在曲轴两端，曲柄转角分别为225°和45°方向加配重块，如图12所示。
7、将修改后的曲轴重新装入装配体中再进行Motion运动仿真（具体步骤见方案二），得出轴承两端受力曲线图，如图13所示。
由曲线图可知，左侧支反力由±1.82×104N 锐减至±0.12×104N, 右侧支反力由±1.84×104N 锐减至 ±0.10×104N，两侧力是大幅减低（降幅约15倍），有效抵消了反作用力矩，这对机组震动是有益的。现将上图中两侧支反力进行矢量叠加，求的合力如图14所示。
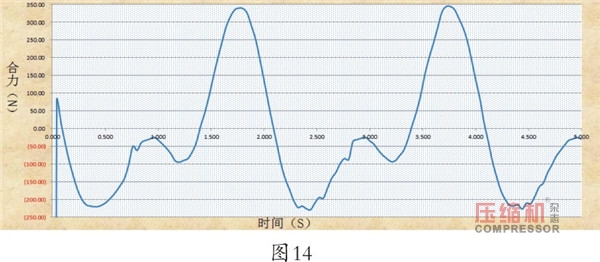
此曲线图表示该运动机构在水平轴（X）方向所受的合力，大小在-250～+350（N）范围内波动。
8、验证一阶惯性矩平衡情况
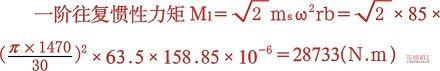
所加配重块质量属性如图15所示。
剩余不平衡力矩△M=M1-M'=400（N.m），此值相对于一阶往复惯性力矩M1非常小（1.4%），可以认为一阶往复惯性力矩被配重块构成的反力矩平衡掉了。
1、达到的技术指标
将修改后的曲轴（图12）进行Simulation有限元分析，具体步骤同方法一，分析结果如图16所示。
2、用途及应用范围
基于SolidWorks的曲轴动平衡仿真可以模拟各类转子动平衡：可适用适有转轴或可装配工艺轴的转子，如nianxiangyuan
及发动机曲轴、机床主轴、滚筒、风机、增压器、电机转子、汽轮机等；也适用于转子本身不具转轴的盘状工件，如离合器、齿轮、风扇、压盘及其总成、制动盘、风叶、水泵叶轮、汽车飞轮、刹车毂、皮带轮、砂轮等盘类零件。
3、经济效益和社会效益
传统硬支撑平衡机虽能较好地对转子本身进行平衡，但是对于转子尺寸相差较大时，往往需要不同规格尺寸的动平衡机，而且试验时仍需将转子从机器上拆下来，这样明显是既不经济，也十分费工。当对曲轴连杆这类特殊转子进行平衡时需要折算连杆作旋转运动质量，一般很难保证精度。
基于SolidWorks的曲轴动平衡仿真则完全可以模拟曲轴运动件受力情况并得出受力曲线图，数据更准确，而且操作简单。这种方法在曲轴设计前期就可以对曲轴进行动平衡分析，提高曲轴设计精度、缩短曲轴开发时间、降低开发成本。尤其对于高速往复式nianxiangyuan
，不仅可以平衡力，而且还可以平衡力矩，确保高速往复式nianxiangyuan
运行平稳，减少轴承磨损，降低噪声。
作者简介：
王孝磊(1986-),男，大学本科，安瑞科（蚌埠）nianxiangyuan
有限公司研发室。
【乐虎集团的官方网站
】某公司因为使用需要，接到任务要求开发一款转速n=1470r/mim，z*大活塞力P=160kN,4M型基础件。这对高转速、4M型的曲轴提出更高的精度要求。
相关人员分析研究后拟利用SolidWorks进行曲轴动平衡仿真，使曲轴达到国际标准ISO1940规定的平衡精度，并选取曲轴精度等级G6.3，依据动平衡原理（要求惯性力和惯性力矩都达到平衡），设计出基于SolidWorks的4M16曲轴动平衡仿真分析报告，并具体提出几种分析方法，以供参考施行研究。
方法一：Simulation有限元分析法
a)夹具：在曲轴两轴承端设置固定铰链，如图1所示。
b) 外部载荷：在旋转轴上添加旋转速度n=1470r/min，方向顺时针（从电机端往曲轴方向看去）如图2所示。
c) 网格化：对曲轴进行网格化，如图3所示。
d)运行并显示结果：如图4所示。
图中显示两端轴承受力情况，得出的合力即为旋转不平衡力F1=221.09N。
方法二：Motion运动分析法
a)新建运动算例，将曲轴两端设好的点分别与机身旋转轴（Z轴）重合。
b)设置旋转马达，转速n=1470r/min，方向顺时针，如图5所示。
c)添加重力：将Y轴正向设为重力方向（因为研究水平轴X方向受力，可以不设置重力），如图6所示。
d)点击计算按钮，输出两端支反力作用曲线图，如图7所示。
e)将左右两侧支反力进行矢量叠加，获得的曲线图如图8所示。
这是一条类正余弦曲线，其极值F2=221N（在水平方向0°和180°）。
方法三：传统计算法
a)原理：具有一定转速的转子，由于材料组织不均性、零件外形误差、装配误差以及结构形状局部不对称性（如键槽）等原因，使通过转子重心的主惯性轴与旋转轴线不重合，因而旋转时，转子产生不平衡离心力，其值如下式所示:
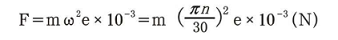
式中：m为转子的重量（kg）；ω为转子角速度（rad/s）；n为转子速度（r/min）；e为转子重心对旋转轴线的偏移，即偏心距（mm）。
b)由曲轴的质量属性可知曲轴质量，重心位置，如图9所示。
c)该曲轴旋转不平衡惯性力
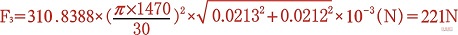
结论
从上述三种方法可知F1=F2=F3=221N，即无论使用Simulation有限元分析法还是Motion运动分析法，其结果与传统计算法得出的结果一致。
确定z*大往复质量Mp
已知电机转速n=1470r/mim，取综合活塞力
P=156kN，λ=0.1724，行程S=2r=2×63.5=127mm，则往复z*大质量Mpmax=P/[rω2（1+λ）]=88.4kg
取往复质量Mp=85kg[相对运动两列的往复运动重量误差，不得大于1磅（0.4536 kg）]
整机进行Motion运动仿真
将连杆、曲轴、活塞及活塞杆等运动件进行装配，在此装配体中进行Motion运动仿真（具体步骤见方法二），得出轴承两端受力曲线图，如图10所示。
从图中可知，左侧受力在±1.82×104 N成正余弦波动，右侧受力在±1.84×104 N成正余弦波动，该力组成的力矩是机组震动的根源。这种周期性变化的支反力是由于一阶惯性力矩不平衡引起的，必须予以降低甚至消除。
4M16曲轴连杆机构受力分析
1、气体力与摩擦力（旋转摩擦力和往复摩擦力）属于内力，它们均在机器内部相互抵消掉。
2、往复惯性力和旋转惯性力属于外力，它们在机器内部若不能平衡掉，那么它们会通过主轴承和机体传递至机器外部来。因为其数值大小和方向随着曲柄转角周期变化，会引起机器的振动和噪声，缩短轴承使用寿命。
3、往复惯性力：往复惯性力的大小由往复质量ms与其加速度a大小决定的，方向同加速度a方向，其表达式为I=msa=msω2r（cosθ+λcos2θ）
4、旋转惯性力：是由曲柄销质量mr沿着旋转轴旋转引起的，方向始终沿着曲柄销半径向外, 其表达式为Ir=mrω2r
5、4M16曲轴连杆机构简图如图11所示：第1列所处位置设为曲柄转角为0，b为相邻列间距，L为两端平衡重距离，δ为1、3列气缸中心线夹角等于90°，λ为1、2列气缸中心线夹角等于180°，其惯性力与惯性力矩如表1所示。
从表1中知旋转惯性力Ir、一阶往复惯性力I1、二阶往复惯性力I2、二阶往复惯性力矩M2均等于零；旋转惯性力矩Mr可在曲柄销对侧加平衡重来平衡（本文曲轴的Mr已配平衡，过程不再赘述）；一阶往复惯性力矩，其极值在曲柄转角45°和225°方向上，故在其反方向225°和45°方向上加配重块进行平衡。一般在曲轴两端，因为此时力臂z*大，则配置块的质量z*轻，对曲轴平衡性能更有利。
，其极值在曲柄转角45°和225°方向上，故在其反方向225°和45°方向上加配重块进行平衡。一般在曲轴两端，因为此时力臂z*大，则配置块的质量z*轻，对曲轴平衡性能更有利。 6、在曲轴两端，曲柄转角分别为225°和45°方向加配重块，如图12所示。
7、将修改后的曲轴重新装入装配体中再进行Motion运动仿真（具体步骤见方案二），得出轴承两端受力曲线图，如图13所示。
由曲线图可知，左侧支反力由±1.82×104N 锐减至±0.12×104N, 右侧支反力由±1.84×104N 锐减至 ±0.10×104N，两侧力是大幅减低（降幅约15倍），有效抵消了反作用力矩，这对机组震动是有益的。现将上图中两侧支反力进行矢量叠加，求的合力如图14所示。
此曲线图表示该运动机构在水平轴（X）方向所受的合力，大小在-250～+350（N）范围内波动。
8、验证一阶惯性矩平衡情况
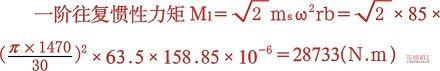
所加配重块质量属性如图15所示。
剩余不平衡力矩△M=M1-M'=400（N.m），此值相对于一阶往复惯性力矩M1非常小（1.4%），可以认为一阶往复惯性力矩被配重块构成的反力矩平衡掉了。
1、达到的技术指标
将修改后的曲轴（图12）进行Simulation有限元分析，具体步骤同方法一，分析结果如图16所示。
2、用途及应用范围
基于SolidWorks的曲轴动平衡仿真可以模拟各类转子动平衡：可适用适有转轴或可装配工艺轴的转子，如nianxiangyuan
及发动机曲轴、机床主轴、滚筒、风机、增压器、电机转子、汽轮机等；也适用于转子本身不具转轴的盘状工件，如离合器、齿轮、风扇、压盘及其总成、制动盘、风叶、水泵叶轮、汽车飞轮、刹车毂、皮带轮、砂轮等盘类零件。
3、经济效益和社会效益
传统硬支撑平衡机虽能较好地对转子本身进行平衡，但是对于转子尺寸相差较大时，往往需要不同规格尺寸的动平衡机，而且试验时仍需将转子从机器上拆下来，这样明显是既不经济，也十分费工。当对曲轴连杆这类特殊转子进行平衡时需要折算连杆作旋转运动质量，一般很难保证精度。
基于SolidWorks的曲轴动平衡仿真则完全可以模拟曲轴运动件受力情况并得出受力曲线图，数据更准确，而且操作简单。这种方法在曲轴设计前期就可以对曲轴进行动平衡分析，提高曲轴设计精度、缩短曲轴开发时间、降低开发成本。尤其对于高速往复式nianxiangyuan
，不仅可以平衡力，而且还可以平衡力矩，确保高速往复式nianxiangyuan
运行平稳，减少轴承磨损，降低噪声。
作者简介：
王孝磊(1986-),男，大学本科，安瑞科（蚌埠）nianxiangyuan
有限公司研发室。
网友评论
条评论
最新评论