【乐虎集团的官方网站
】美国石油学会(API)最近实施了离心式nianxiangyuan
转子动力学稳定性的新规范,规范包含了Level I。作为迷宫密封和气动激励的不稳定效应的近似,修正的Alford方程用于估计不稳定的影响作用。如果nianxiangyuan
不满足Level I规范,那就采用更复杂的Level II分析,这需要更详细的迷宫密封分析。
本文考虑了现代高压离心nianxiangyuan
的五个典型不稳定情况的实例。在应用API I级和II级稳定性分析后,进行了设计更改优化以稳定nianxiangyuan
。对于这些情况,API稳定性规范用于识别对转子稳定性影响最大的部件。对平衡活塞密封和叶轮密封进行了具体详细的分析。将修正的Alford方程应用于多级nianxiangyuan
,用于分析其适用性,并与全迷宫密封分析进行了比较。讨论了迷宫密封分析的重要因素,如密封间隙效应、入口涡流效应、间隙效应。最后,提出了一种计算迷宫密封交叉耦合力的方法。对于所有五个实例nianxiangyuan
,与迷宫计算力相比,修正的Alford力将导致出现最差的稳定性水平。
前言
随着转速和额定功率的提高,离心nianxiangyuan
的转子不稳定性成为20世纪60年代的一个主要问题。不稳定的nianxiangyuan
具有很高的次同步振动,其振动频率与转子的第一基本固有频率一致。20世纪70年代初,两个著名和经典的离心nianxiangyuan
不稳定情况被称为Kaybob(史米斯,1975;FoeLee and Males,1975)和Ekofisk(Grouy, 等人,1976)。这两个问题的解决方案代价高昂,费时费力,最终对转子进行了重新设计。
基于这些经验结果,转子系统稳定性的评估已经成为转子动力学分析和旋转机械设计的重要部分。最常见的是,最低或第一模态,对应于转子的第一基本固有频率,再次被激发后,将导致次同步振动和转子不稳定。稳定性或阻尼固有频率分析的主要结果是对方程解的根值或特征值的处理,一方面通过实部进行稳定性预测,另一方面,通过虚部来预测不稳定频率。
本文的主要目的是考察几种工业离心nianxiangyuan
的稳定性结果。通过与Kirk(1988a,1988b,1990)的API Level II的迷宫密封计算力的比较,对API Level I修正的Alford交叉耦合力进行了计算,以确定它是否确实可近似为一个保守的nianxiangyuan
失稳力。此外,进行了详细的迷宫密封分析,以确定哪些参数是影响离心nianxiangyuan
稳定性的关键因素,主要包括轴承间隙公差范围、迷宫密封间隙和迷宫密封入口涡流效应等参数。
KAYBOB不稳定性
首先将简要介绍Kaybob不稳定性(Smith,1975;FoeLee and Males,1975)。该九级低压天然气喷射nianxiangyuan
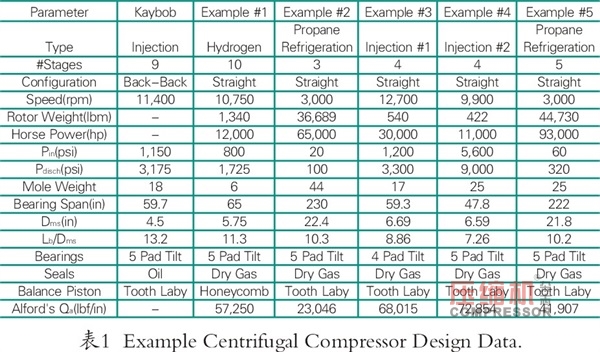
于1971在加拿大阿尔伯塔投产。关键运行参数总结在表1中。最大持续速度(MCS)为11400rpm,入口压力1150 psi,出口压力3175 psi,18MW气体。轴承跨度Lb,与中轴直径Dms之比为13.2,表明轴非常的有弹性。nianxiangyuan
的横截面如图1所示。
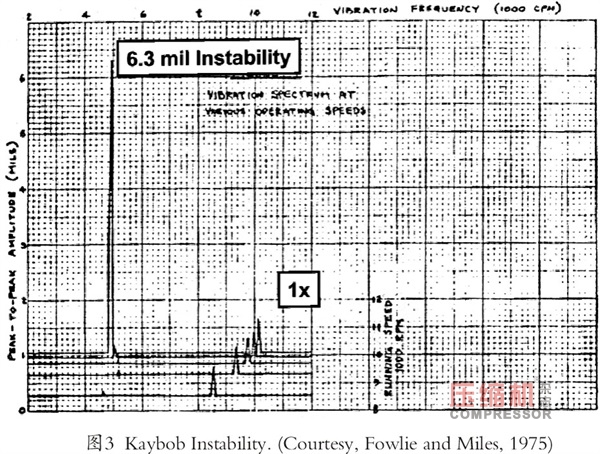
 不稳定性的严重程度可以在图2的轴心轨迹上看到。通过观察,五瓦块可倾瓦滑动轴承的轮廓线在6×9mils的峰-峰值轴心轨迹图中非常明显。图3中,突然出现的6.3mils的不稳定现象,显然是一种次同步振动,是由激发起的nianxiangyuan
一阶临界转速所致。
不稳定性的严重程度可以在图2的轴心轨迹上看到。通过观察,五瓦块可倾瓦滑动轴承的轮廓线在6×9mils的峰-峰值轴心轨迹图中非常明显。图3中,突然出现的6.3mils的不稳定现象,显然是一种次同步振动,是由激发起的nianxiangyuan
一阶临界转速所致。

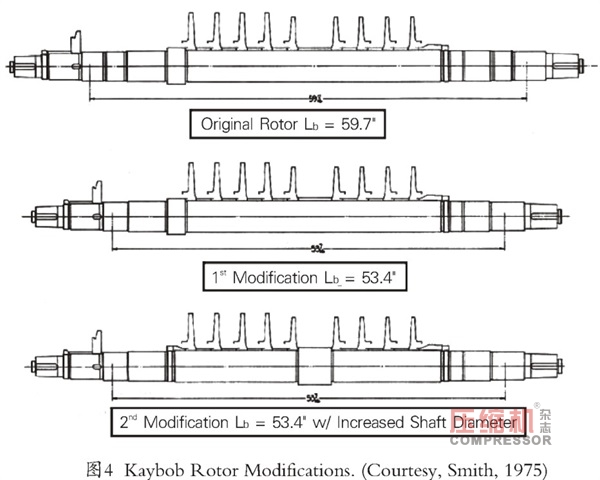
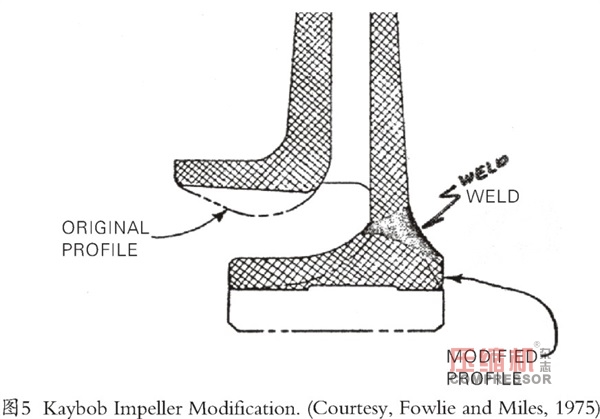
 消除不稳定性的尝试包括轴承重新设计、油封修改、迷宫密封修改、平衡活塞修改、无叶扩散器改型、挤压油膜阻尼器改型,以及最后至少两个转子重新设计(图4)。第二转子重新设计包括增加中轴直径。最初,使用现有的叶轮锻件,切割和焊接叶轮轮毂,以增加叶轮内径以适应轴直径的增加(图5)。
消除不稳定性的尝试包括轴承重新设计、油封修改、迷宫密封修改、平衡活塞修改、无叶扩散器改型、挤压油膜阻尼器改型,以及最后至少两个转子重新设计(图4)。第二转子重新设计包括增加中轴直径。最初,使用现有的叶轮锻件,切割和焊接叶轮轮毂,以增加叶轮内径以适应轴直径的增加(图5)。
 显然,这种努力代价高昂。然而,它与Ekofisk不稳定性问题一起,提供了改进分析的可能,最终呈现出来现有的稳定性和迷宫密封型式以及新的API稳定性规范。
显然,这种努力代价高昂。然而,它与Ekofisk不稳定性问题一起,提供了改进分析的可能,最终呈现出来现有的稳定性和迷宫密封型式以及新的API稳定性规范。
对数衰减率
稳定性分析和API稳定性验收准则的关键参数是对数衰减率。对数衰减率是自由振荡衰减率的量度,也是确定系统中存在的阻尼参数的简便方法。阻尼值越大,衰减率越快,系统的稳定性也越好。
对数衰减率被定义为任何两个连续振幅的比值的自然对数。参考图6,对数衰减率定义为:
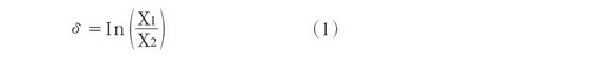
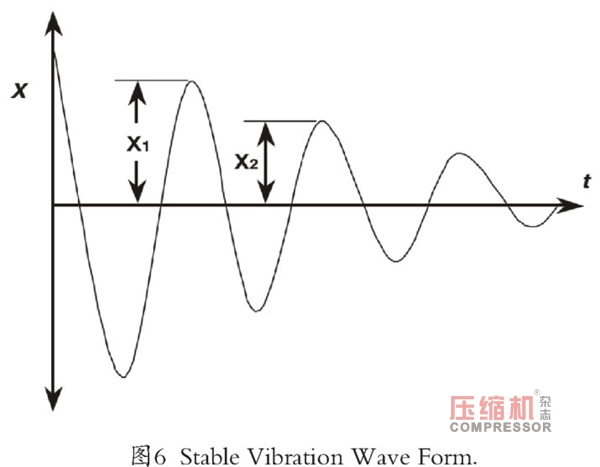 对于稳定的系统,具有正的衰减速率,对数衰减率为正。对于具有负衰减率的不稳定系统,对数衰减率为负。具有正对数衰减率的稳定系统包含足够的阻尼来克服初始激励。由此产生的位移将随着时间消散。相反,对数衰减率为负值的不稳定系统,没有足够的阻尼来克服初始激励,随着时间的推移将导致位移增加。
对数衰减率也可以用特征值的实部s和虚部ωd表达:
对于稳定的系统,具有正的衰减速率,对数衰减率为正。对于具有负衰减率的不稳定系统,对数衰减率为负。具有正对数衰减率的稳定系统包含足够的阻尼来克服初始激励。由此产生的位移将随着时间消散。相反,对数衰减率为负值的不稳定系统,没有足够的阻尼来克服初始激励,随着时间的推移将导致位移增加。
对数衰减率也可以用特征值的实部s和虚部ωd表达:
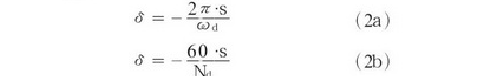 有阻尼固有频率可以有两种表达,或采用ωd,单位为rad/s,或采用Nd,单位为rpm。
例1: 12000HP,10级氢离心nianxiangyuan
第一个例子是一个10级12000马力氢离心nianxiangyuan
,具有65英寸的轴承跨度,Lb/Dms为11.3。转子重1340磅,在10750转/分的最大持续速度(MCS)下运行,干气密封和五瓦块可倾瓦滑动轴承如表1。
有阻尼固有频率可以有两种表达,或采用ωd,单位为rad/s,或采用Nd,单位为rpm。
例1: 12000HP,10级氢离心nianxiangyuan
第一个例子是一个10级12000马力氢离心nianxiangyuan
,具有65英寸的轴承跨度,Lb/Dms为11.3。转子重1340磅,在10750转/分的最大持续速度(MCS)下运行,干气密封和五瓦块可倾瓦滑动轴承如表1。
入口压力为800 psi,排气压力为1725 psi,气体摩尔质量为6。对数衰减率在零气动交叉耦合刚度下,在最小轴承间隙下Q为0.26,在最大轴承间隙下为0.40。从API规范617,第七版(2002),修正的Alford方程是:
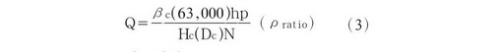 βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每级的Q均可由上述公式计算。由于每级的密度比和马力并不完全一致,因此每级马力被假定为上述总值的十分之一。每级密度比按上述总密度比假定,达到1/10的功率。叶轮出口宽度和叶轮直径是级间变量。所有10个Q值的总和是API Alford计算出来的,预期的交叉耦合值Qa为57250lbf/in。QA集中在转子中跨,得到的对数衰减率为:最小轴承间隙下为-0.4,最大轴承间隙下为-0.23。而API稳定性判定准则是对数衰减率大于0.1。因此,需要进行II级分析。
在进行分析之前,已经决定在平衡活塞上使用蜂窝密封。因此,上文中的稳定性结果包括蜂窝密封动态特性(Scharrer and Pelletti, 1994)。
以迷宫密封几何形状、级气体特性和级压力作为输入,对10个叶轮密封件中的每一个进行迷宫密封分析(Kirk,1990)。在密封入口处的气体涡流值被假定为0.6(对应于转速的60%)。保守起见,考虑密封件和密封套的加工公差范围,使用最小的密封间隙。10个迷宫密封总的Q为15700lbf/in。
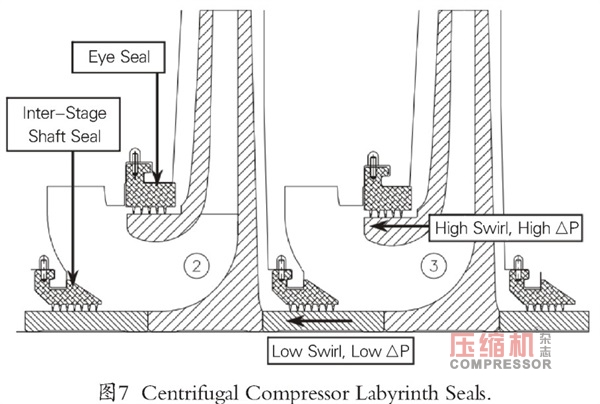
忽略轴上密封作用,因为此处压降值很低。另外,密封流从静止部分进入密封,因此,入口涡流值低于密封涡流(图7)。高入口涡流将导致高Q值。
βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每级的Q均可由上述公式计算。由于每级的密度比和马力并不完全一致,因此每级马力被假定为上述总值的十分之一。每级密度比按上述总密度比假定,达到1/10的功率。叶轮出口宽度和叶轮直径是级间变量。所有10个Q值的总和是API Alford计算出来的,预期的交叉耦合值Qa为57250lbf/in。QA集中在转子中跨,得到的对数衰减率为:最小轴承间隙下为-0.4,最大轴承间隙下为-0.23。而API稳定性判定准则是对数衰减率大于0.1。因此,需要进行II级分析。
在进行分析之前,已经决定在平衡活塞上使用蜂窝密封。因此,上文中的稳定性结果包括蜂窝密封动态特性(Scharrer and Pelletti, 1994)。
以迷宫密封几何形状、级气体特性和级压力作为输入,对10个叶轮密封件中的每一个进行迷宫密封分析(Kirk,1990)。在密封入口处的气体涡流值被假定为0.6(对应于转速的60%)。保守起见,考虑密封件和密封套的加工公差范围,使用最小的密封间隙。10个迷宫密封总的Q为15700lbf/in。
忽略轴上密封作用,因为此处压降值很低。另外,密封流从静止部分进入密封,因此,入口涡流值低于密封涡流(图7)。高入口涡流将导致高Q值。
 由于总的密封Q集中在转子中心,因此得到的对数衰减率,对应于最小轴承间隙为0.08,对应于最大轴承间隙为0.28。
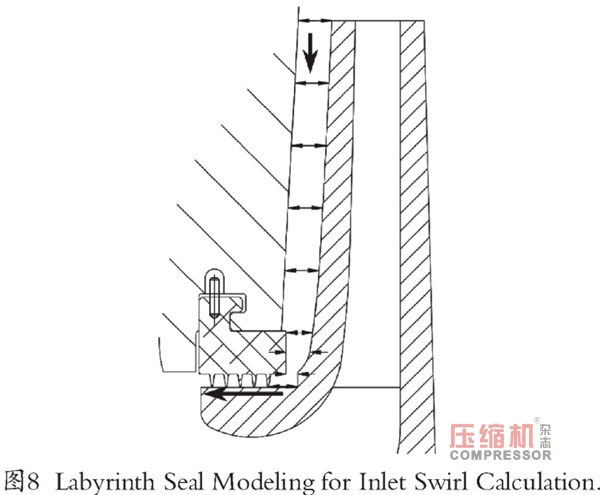
除了估计迷宫密封处的入口涡流,还可以通过模拟叶轮表面和静止件之间的间隙来计算,如图8(Kirk,1990)。随着叶轮间隙模型的引入,入口涡流计算值为0.52,得到的Q值为7600 Lbf/in时的所有密封。由于总的密封Q集中在转子中心,所得对数衰减率值分别为:最小轴承间隙为0.17,最大轴承间隙为0.35。与I级分析一样,II级的API稳定性验收准则是大于0.1的对数衰减率。因此,该nianxiangyuan
在轴承间隙公差范围内满足API要求。
由于总的密封Q集中在转子中心,因此得到的对数衰减率,对应于最小轴承间隙为0.08,对应于最大轴承间隙为0.28。
除了估计迷宫密封处的入口涡流,还可以通过模拟叶轮表面和静止件之间的间隙来计算,如图8(Kirk,1990)。随着叶轮间隙模型的引入,入口涡流计算值为0.52,得到的Q值为7600 Lbf/in时的所有密封。由于总的密封Q集中在转子中心,所得对数衰减率值分别为:最小轴承间隙为0.17,最大轴承间隙为0.35。与I级分析一样,II级的API稳定性验收准则是大于0.1的对数衰减率。因此,该nianxiangyuan
在轴承间隙公差范围内满足API要求。
 结果如表2所示,分别在图9和图10中给出了最小和最大轴承间隙。从图9和图10中也可以注意到零对数衰减率时的Q值,Q0。这些分别为22500和40000lbf/in的最小和最大轴承间隙。显然,使用改进的Alford力预测的稳定性水平较为保守。
结果如表2所示,分别在图9和图10中给出了最小和最大轴承间隙。从图9和图10中也可以注意到零对数衰减率时的Q值,Q0。这些分别为22500和40000lbf/in的最小和最大轴承间隙。显然,使用改进的Alford力预测的稳定性水平较为保守。

 密封入口涡流效应
入口涡流对总密封Q的影响如图11所示。在图12中给出了相应的稳定性影响。需要注意的是,在最小轴承和密封间隙下,入口涡流值为0.3时,对数衰减率将提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)
密封入口涡流效应
入口涡流对总密封Q的影响如图11所示。在图12中给出了相应的稳定性影响。需要注意的是,在最小轴承和密封间隙下,入口涡流值为0.3时,对数衰减率将提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)

 密封间隙效应
密封间隙对Q的影响如图13所示。加工直径公差范围为16~20mils。假设由于叶轮的离心膨胀,最小直径密封间隙减小4mils,图13也给出了直径为12mils的最小工作间隙。图14中给出了入口涡流为0.6和最小轴承间隙时对稳定性的影响作用。
密封间隙效应
密封间隙对Q的影响如图13所示。加工直径公差范围为16~20mils。假设由于叶轮的离心膨胀,最小直径密封间隙减小4mils,图13也给出了直径为12mils的最小工作间隙。图14中给出了入口涡流为0.6和最小轴承间隙时对稳定性的影响作用。

 图15说明了收敛和发散型密封间隙对稳定性的影响。假设所有密封齿均为12mils的直径间隙,得到的对数衰减率为0.6。如果间隙从密封入口(直径为16mils)收敛到出口(直径为8mils),那么对数衰减率将减小到-0.11。反之,从入口(直径为8mils)到出口(直径为16mils),那么对数衰减率为0.23。这些计算值的前提条件是:假定最小轴承间隙,并且入口涡流值为0.6。
图15说明了收敛和发散型密封间隙对稳定性的影响。假设所有密封齿均为12mils的直径间隙,得到的对数衰减率为0.6。如果间隙从密封入口(直径为16mils)收敛到出口(直径为8mils),那么对数衰减率将减小到-0.11。反之,从入口(直径为8mils)到出口(直径为16mils),那么对数衰减率为0.23。这些计算值的前提条件是:假定最小轴承间隙,并且入口涡流值为0.6。
 显然,应该优选发散型的间隙分布,以提高稳定性。对发散型间隙而言,虽然密封主刚度为负,这种影响是最小的。此外,对于发散型间隙情况,泄漏量实际上比恒定间隙减小了。对于这种nianxiangyuan
,从密封出口位置增加到密封入口位置,叶轮随转速的增大而变化,从而产生不同的密封间隙。
对于发散间隙,这种影响是最小的。此外,泄漏量实际上比恒定间隙减小了发散间隙情况。对于这种nianxiangyuan
,叶轮的增长速度从眼睛密封排放位置(叶轮眼)增加到眼睛密封入口位置,从而产生不同的密封间隙。
平衡活塞蜂窝密封
堵塞与入口涡流效应
蜂窝密封的一个问题是蜂窝孔可能堵塞或填充多余物。其它非迷宫式密封也可能存在堵塞,例如孔型密封件。
蜂窝密封的这种堵塞孔效应如图16所示,图中给出了最小轴承间隙,以及三个不同的蜂窝密封入口涡流值:0.8,一个较糟糕的值;0.6,一个更现实的值;和0.3,模拟包含涡流制动器。结果表明,随着蜂窝孔的填充或堵塞,稳定性降低。对于入口涡流为0.6的情况,只要有小于48%的孔隙填充,则对数衰减率就会大于0.1,满足API要求。对于包含涡流制动器(入口涡流为0.3),只要孔隙填充数少于60%,对数衰减率就大于0.1。
显然,应该优选发散型的间隙分布,以提高稳定性。对发散型间隙而言,虽然密封主刚度为负,这种影响是最小的。此外,对于发散型间隙情况,泄漏量实际上比恒定间隙减小了。对于这种nianxiangyuan
,从密封出口位置增加到密封入口位置,叶轮随转速的增大而变化,从而产生不同的密封间隙。
对于发散间隙,这种影响是最小的。此外,泄漏量实际上比恒定间隙减小了发散间隙情况。对于这种nianxiangyuan
,叶轮的增长速度从眼睛密封排放位置(叶轮眼)增加到眼睛密封入口位置,从而产生不同的密封间隙。
平衡活塞蜂窝密封
堵塞与入口涡流效应
蜂窝密封的一个问题是蜂窝孔可能堵塞或填充多余物。其它非迷宫式密封也可能存在堵塞,例如孔型密封件。
蜂窝密封的这种堵塞孔效应如图16所示,图中给出了最小轴承间隙,以及三个不同的蜂窝密封入口涡流值:0.8,一个较糟糕的值;0.6,一个更现实的值;和0.3,模拟包含涡流制动器。结果表明,随着蜂窝孔的填充或堵塞,稳定性降低。对于入口涡流为0.6的情况,只要有小于48%的孔隙填充,则对数衰减率就会大于0.1,满足API要求。对于包含涡流制动器(入口涡流为0.3),只要孔隙填充数少于60%,对数衰减率就大于0.1。
 例2:65000 马力,3级丙烷制冷nianxiangyuan
第二个例子是用于制冷的三级、三段65000 马力丙烷nianxiangyuan
,其具有230inch的轴承跨度和Lb/Dms=10.3。转子的重量超过36000磅,工作转速3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为20 psi,出口压力为100 psi,气体摩尔重量为44。大型制冷nianxiangyuan
的典型特征是具有较低的对数衰减率和相对较小的不稳定力表现。这台机器也不例外。该nianxiangyuan
的基本对数衰减率(仅就转子和轴承而言,Q=0)在轴承公差范围内分布于0.18到0.13不等。
过去对具有多过程段的nianxiangyuan
,在考虑“Wachel”型方程(Wachel和Von Nimz,1981)时,出现了适用性问题。在大多数情况下,通过逐级应用修正的Alford方程,已经解决了这些问题。在该应用中,每级表示一个过程段,该过程段内将侧流添加到主流中,这发生在第二叶轮和第三叶轮之前。图17给出了nianxiangyuan
的转子动力学模型。
例2:65000 马力,3级丙烷制冷nianxiangyuan
第二个例子是用于制冷的三级、三段65000 马力丙烷nianxiangyuan
,其具有230inch的轴承跨度和Lb/Dms=10.3。转子的重量超过36000磅,工作转速3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为20 psi,出口压力为100 psi,气体摩尔重量为44。大型制冷nianxiangyuan
的典型特征是具有较低的对数衰减率和相对较小的不稳定力表现。这台机器也不例外。该nianxiangyuan
的基本对数衰减率(仅就转子和轴承而言,Q=0)在轴承公差范围内分布于0.18到0.13不等。
过去对具有多过程段的nianxiangyuan
,在考虑“Wachel”型方程(Wachel和Von Nimz,1981)时,出现了适用性问题。在大多数情况下,通过逐级应用修正的Alford方程,已经解决了这些问题。在该应用中,每级表示一个过程段,该过程段内将侧流添加到主流中,这发生在第二叶轮和第三叶轮之前。图17给出了nianxiangyuan
的转子动力学模型。

 应用公式(3),可以计算预期的不稳定力Qa,总预期的失稳力Qa为23046 lbf/in。将这应用于转子中心,分别得到最小和最大轴承刚度的对数衰减率为0.15和0.09。图18显示了稳定性灵敏度曲线。(轴承间隙和油入口温度的公差范围限定了轴承刚度的范围)。根据API的要求,由于最坏情况δa<0.1,用Kirk(1990)开发的方法进行二级分析,以预测叶轮迷宫式密封件的性能。这些不稳定力被施加在密封的实际位置上。对于相同范围内的轴承刚度,对数衰减率是针对以下条件计算的:
仅转子和轴承
转子、轴承和叶轮迷宫密封
转子、轴承、叶轮迷宫密封和平衡活塞
表3包含了二级分析的结果和使用修正的Alford力对转子稳定性的估计。正如预期的那样,由于迷宫密封(包括平衡活塞)的激励力很小,因此对转子稳定性影响较小。对于这个应用,使用改进的Alford力预测的稳定性水平是保守的。
应用公式(3),可以计算预期的不稳定力Qa,总预期的失稳力Qa为23046 lbf/in。将这应用于转子中心,分别得到最小和最大轴承刚度的对数衰减率为0.15和0.09。图18显示了稳定性灵敏度曲线。(轴承间隙和油入口温度的公差范围限定了轴承刚度的范围)。根据API的要求,由于最坏情况δa<0.1,用Kirk(1990)开发的方法进行二级分析,以预测叶轮迷宫式密封件的性能。这些不稳定力被施加在密封的实际位置上。对于相同范围内的轴承刚度,对数衰减率是针对以下条件计算的:
仅转子和轴承
转子、轴承和叶轮迷宫密封
转子、轴承、叶轮迷宫密封和平衡活塞
表3包含了二级分析的结果和使用修正的Alford力对转子稳定性的估计。正如预期的那样,由于迷宫密封(包括平衡活塞)的激励力很小,因此对转子稳定性影响较小。对于这个应用,使用改进的Alford力预测的稳定性水平是保守的。
 例3 30000马力4级喷射nianxiangyuan
(略)
第四个例子是11000马力的四级离心nianxiangyuan
,用于喷射,具有48英寸的轴承跨度,Lb/Dms=7.26。转子重422磅,运行转速为9900rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为5600 psi,出口压力为9000 psi。
就喷射方面而言,该nianxiangyuan
被认为具有较高的排放压力范围和中等的功率与重量比值。在这样的情况下,由于nianxiangyuan
中气体的密度升高,不稳定力预计会更高。实际上,由于平均气体密度为115 kg/m3,需要进行II级分析。如前所述,制造商保守地设计了具有较大中心轴段的nianxiangyuan
,以抵消预期的更高的不稳定力(图19)。
例3 30000马力4级喷射nianxiangyuan
(略)
第四个例子是11000马力的四级离心nianxiangyuan
,用于喷射,具有48英寸的轴承跨度,Lb/Dms=7.26。转子重422磅,运行转速为9900rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为5600 psi,出口压力为9000 psi。
就喷射方面而言,该nianxiangyuan
被认为具有较高的排放压力范围和中等的功率与重量比值。在这样的情况下,由于nianxiangyuan
中气体的密度升高,不稳定力预计会更高。实际上,由于平均气体密度为115 kg/m3,需要进行II级分析。如前所述,制造商保守地设计了具有较大中心轴段的nianxiangyuan
,以抵消预期的更高的不稳定力(图19)。
 这种情况下,修改后的Alford力计算值为72854lbf/in,大致等于示例3中的nianxiangyuan
。(图20)。较高的气体密度抵消了前面例子中较高的马力。因此,对于这两个例子,预期的不稳定力水平大致相同。表3包含了I级和II级分析的稳定性分析结果。与其它喷射nianxiangyuan
一样,由于Q0<2Qa,需要进行II级分析,这表明预期的失稳力和驱动系统不稳定所需的量之间存在足够的安全余量。
这种情况下,修改后的Alford力计算值为72854lbf/in,大致等于示例3中的nianxiangyuan
。(图20)。较高的气体密度抵消了前面例子中较高的马力。因此,对于这两个例子,预期的不稳定力水平大致相同。表3包含了I级和II级分析的稳定性分析结果。与其它喷射nianxiangyuan
一样,由于Q0<2Qa,需要进行II级分析,这表明预期的失稳力和驱动系统不稳定所需的量之间存在足够的安全余量。
 如前所述,对于两个喷射nianxiangyuan
来说,Alford不稳定力几乎相等。表3通过比较两个II级分析,证实了这一事实。从基础值到包括所有不稳定力条件,在轴承系数变化范围内,对于第一喷射nianxiangyuan
的对数衰减率大约为-0.55和-0.40,对于第二喷射nianxiangyuan
的对数衰减率约为-0.45和-0.30。考虑到转子和轴承几何形状的差异,这两者可视为相当或一致。与前面的例子不同,平衡活塞产生了大部分的不稳定力。
由于nianxiangyuan
内气体平均密度上升,因此需要进行II级分析。这台nianxiangyuan
成功地通过了满负荷试验,没有发生稳定性问题。
例5 混合制冷
在前三个例子中,通过比较I级和II级分析,得到了对数衰减率值,来确定修正的Alford方程的保守性。在本节中,提出了一种比较等效集中不稳定力的更直接的方法,类似于Memmott (2000)。示例3中,喷射nianxiangyuan
与较大的制冷nianxiangyuan
一起使用。93000马力的混合制冷nianxiangyuan
(例5)具有222英寸的轴承跨度,Lb/Dms为10.2。图21比较了这两种nianxiangyuan
。转子重44730磅,运行转速为3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为60 psi,使用25MW的气体,具有320 psi的出口压力。
如前所述,对于两个喷射nianxiangyuan
来说,Alford不稳定力几乎相等。表3通过比较两个II级分析,证实了这一事实。从基础值到包括所有不稳定力条件,在轴承系数变化范围内,对于第一喷射nianxiangyuan
的对数衰减率大约为-0.55和-0.40,对于第二喷射nianxiangyuan
的对数衰减率约为-0.45和-0.30。考虑到转子和轴承几何形状的差异,这两者可视为相当或一致。与前面的例子不同,平衡活塞产生了大部分的不稳定力。
由于nianxiangyuan
内气体平均密度上升,因此需要进行II级分析。这台nianxiangyuan
成功地通过了满负荷试验,没有发生稳定性问题。
例5 混合制冷
在前三个例子中,通过比较I级和II级分析,得到了对数衰减率值,来确定修正的Alford方程的保守性。在本节中,提出了一种比较等效集中不稳定力的更直接的方法,类似于Memmott (2000)。示例3中,喷射nianxiangyuan
与较大的制冷nianxiangyuan
一起使用。93000马力的混合制冷nianxiangyuan
(例5)具有222英寸的轴承跨度,Lb/Dms为10.2。图21比较了这两种nianxiangyuan
。转子重44730磅,运行转速为3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为60 psi,使用25MW的气体,具有320 psi的出口压力。
 为了产生与修正的Alford方程计算等效的失稳力,使用以下关系计算每个密封件的等效交叉耦合刚度:
为了产生与修正的Alford方程计算等效的失稳力,使用以下关系计算每个密封件的等效交叉耦合刚度:
 K和C值由迷宫密封分析(Kirk, 1990)确定,转子中心的等效模态交叉耦合定义为:
K和C值由迷宫密封分析(Kirk, 1990)确定,转子中心的等效模态交叉耦合定义为:
 从第一阻尼固有频率的归一化模态振型确定模态影响因子Mf,表征密封位置处的位移。对所有密封位置进行求和,得到交叉耦合力。这种模态交叉耦合,Qm,连同II级分析中计算的对数衰减率值一起,在最大轴承刚度的条件下,绘制在两个nianxiangyuan
实例的稳定性灵敏度图上。
图22为例子3种第一种喷射nianxiangyuan
的结果。
从第一阻尼固有频率的归一化模态振型确定模态影响因子Mf,表征密封位置处的位移。对所有密封位置进行求和,得到交叉耦合力。这种模态交叉耦合,Qm,连同II级分析中计算的对数衰减率值一起,在最大轴承刚度的条件下,绘制在两个nianxiangyuan
实例的稳定性灵敏度图上。
图22为例子3种第一种喷射nianxiangyuan
的结果。

 该nianxiangyuan
的最小模态系数仅为0.91,反映了nianxiangyuan
的轴具有较好的刚性工作条件(stiffer shaft operation)。考虑到迷宫密封和平衡活塞力,计算模态交叉耦合系数为44933lbf/in。表3中,包括所有不稳定力的II级对数衰减率,在最大支承刚度时,为0.48。在灵敏度图上绘制这一点,人们发现该点几乎直接位于通过在转子中心放置不同量值的交叉耦合刚度而得到的直线上。需要强调的是,对数衰减率绘制的δm是由II级分析计算得到的,考虑位于实际位置的密封效应。从这一点可以得出如下结论:
modal reduction产生的交叉耦合力直接与修正Alford力相媲美。
模态交叉耦合还提供了基于实际密封系数的转子裕度指示。(在这种情况下,将44933 lbf/in与95300lbf/in的Q0量进行比较。大约存在两倍安全余量,或更简单地说,迷宫密封的不稳定效应可能比预测不稳定条件之前的计算值大两倍。
对混合制冷nianxiangyuan
进行重复计算(例5)。对于这种nianxiangyuan
,最小模态系数为0.56,表示轴具有更灵活的弯曲模态。在II级分析中包括两种密封结构,一种具有分流的平衡活塞另一种是没有分流的密封。模态交叉耦合和最终II级对数衰减率值绘制如图23所示。与喷射nianxiangyuan
一样,这两个点与I级分析的灵敏度线密切相关。这是真实的情况,即使在分流平衡活塞的情况下,净交叉耦合项为负(或稳定)。
结论
开展了API水平I级修正的Alford交叉耦合力的计算,并证实了nianxiangyuan
的不稳定力是一种保守估计。研究了几个工业领域的应用,包括氢nianxiangyuan
、两个高压喷射nianxiangyuan
、一个具有高功率与重量比的nianxiangyuan
,以及两个大型制冷nianxiangyuan
,包括多级结构。在所有情况下,修正的Alford力,将产生最差的稳定性水平。
此外,检查了II级分析的细节,以确定哪些参数是确定离心nianxiangyuan
稳定性的关键。一些已知的影响,包括轴承间隙公差和迷宫密封入口涡流,显示出对10级氢气nianxiangyuan
的稳定性水平有重大影响。在恒定的入口涡流为0.6的情况下,仅仅将在叶轮密封处的齿隙倾斜从8 mils 径向收敛区变为8 mils径向发散区,预测的对数衰减率将从-0.11变为0.23。这为提高离心式离心nianxiangyuan
的稳定性提供了另一个简单的途径。
最后,提出了一种模态方法来直接比较I级和II级不稳定力。除了确认修正的Alford力的保守性外,模态方法还允许使用稳定性灵敏度曲线来逼近迷宫密封系数相对于零对数衰减率阈值的安全裕度。
参数如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)
该nianxiangyuan
的最小模态系数仅为0.91,反映了nianxiangyuan
的轴具有较好的刚性工作条件(stiffer shaft operation)。考虑到迷宫密封和平衡活塞力,计算模态交叉耦合系数为44933lbf/in。表3中,包括所有不稳定力的II级对数衰减率,在最大支承刚度时,为0.48。在灵敏度图上绘制这一点,人们发现该点几乎直接位于通过在转子中心放置不同量值的交叉耦合刚度而得到的直线上。需要强调的是,对数衰减率绘制的δm是由II级分析计算得到的,考虑位于实际位置的密封效应。从这一点可以得出如下结论:
modal reduction产生的交叉耦合力直接与修正Alford力相媲美。
模态交叉耦合还提供了基于实际密封系数的转子裕度指示。(在这种情况下,将44933 lbf/in与95300lbf/in的Q0量进行比较。大约存在两倍安全余量,或更简单地说,迷宫密封的不稳定效应可能比预测不稳定条件之前的计算值大两倍。
对混合制冷nianxiangyuan
进行重复计算(例5)。对于这种nianxiangyuan
,最小模态系数为0.56,表示轴具有更灵活的弯曲模态。在II级分析中包括两种密封结构,一种具有分流的平衡活塞另一种是没有分流的密封。模态交叉耦合和最终II级对数衰减率值绘制如图23所示。与喷射nianxiangyuan
一样,这两个点与I级分析的灵敏度线密切相关。这是真实的情况,即使在分流平衡活塞的情况下,净交叉耦合项为负(或稳定)。
结论
开展了API水平I级修正的Alford交叉耦合力的计算,并证实了nianxiangyuan
的不稳定力是一种保守估计。研究了几个工业领域的应用,包括氢nianxiangyuan
、两个高压喷射nianxiangyuan
、一个具有高功率与重量比的nianxiangyuan
,以及两个大型制冷nianxiangyuan
,包括多级结构。在所有情况下,修正的Alford力,将产生最差的稳定性水平。
此外,检查了II级分析的细节,以确定哪些参数是确定离心nianxiangyuan
稳定性的关键。一些已知的影响,包括轴承间隙公差和迷宫密封入口涡流,显示出对10级氢气nianxiangyuan
的稳定性水平有重大影响。在恒定的入口涡流为0.6的情况下,仅仅将在叶轮密封处的齿隙倾斜从8 mils 径向收敛区变为8 mils径向发散区,预测的对数衰减率将从-0.11变为0.23。这为提高离心式离心nianxiangyuan
的稳定性提供了另一个简单的途径。
最后,提出了一种模态方法来直接比较I级和II级不稳定力。除了确认修正的Alford力的保守性外,模态方法还允许使用稳定性灵敏度曲线来逼近迷宫密封系数相对于零对数衰减率阈值的安全裕度。
参数如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)
【乐虎集团的官方网站
】美国石油学会(API)最近实施了离心式nianxiangyuan
转子动力学稳定性的新规范,规范包含了Level I。作为迷宫密封和气动激励的不稳定效应的近似,修正的Alford方程用于估计不稳定的影响作用。如果nianxiangyuan
不满足Level I规范,那就采用更复杂的Level II分析,这需要更详细的迷宫密封分析。
本文考虑了现代高压离心nianxiangyuan
的五个典型不稳定情况的实例。在应用API I级和II级稳定性分析后,进行了设计更改优化以稳定nianxiangyuan
。对于这些情况,API稳定性规范用于识别对转子稳定性影响最大的部件。对平衡活塞密封和叶轮密封进行了具体详细的分析。将修正的Alford方程应用于多级nianxiangyuan
,用于分析其适用性,并与全迷宫密封分析进行了比较。讨论了迷宫密封分析的重要因素,如密封间隙效应、入口涡流效应、间隙效应。最后,提出了一种计算迷宫密封交叉耦合力的方法。对于所有五个实例nianxiangyuan
,与迷宫计算力相比,修正的Alford力将导致出现最差的稳定性水平。
前言
随着转速和额定功率的提高,离心nianxiangyuan
的转子不稳定性成为20世纪60年代的一个主要问题。不稳定的nianxiangyuan
具有很高的次同步振动,其振动频率与转子的第一基本固有频率一致。20世纪70年代初,两个著名和经典的离心nianxiangyuan
不稳定情况被称为Kaybob(史米斯,1975;FoeLee and Males,1975)和Ekofisk(Grouy, 等人,1976)。这两个问题的解决方案代价高昂,费时费力,最终对转子进行了重新设计。
基于这些经验结果,转子系统稳定性的评估已经成为转子动力学分析和旋转机械设计的重要部分。最常见的是,最低或第一模态,对应于转子的第一基本固有频率,再次被激发后,将导致次同步振动和转子不稳定。稳定性或阻尼固有频率分析的主要结果是对方程解的根值或特征值的处理,一方面通过实部进行稳定性预测,另一方面,通过虚部来预测不稳定频率。
本文的主要目的是考察几种工业离心nianxiangyuan
的稳定性结果。通过与Kirk(1988a,1988b,1990)的API Level II的迷宫密封计算力的比较,对API Level I修正的Alford交叉耦合力进行了计算,以确定它是否确实可近似为一个保守的nianxiangyuan
失稳力。此外,进行了详细的迷宫密封分析,以确定哪些参数是影响离心nianxiangyuan
稳定性的关键因素,主要包括轴承间隙公差范围、迷宫密封间隙和迷宫密封入口涡流效应等参数。
KAYBOB不稳定性
首先将简要介绍Kaybob不稳定性(Smith,1975;FoeLee and Males,1975)。该九级低压天然气喷射nianxiangyuan
于1971在加拿大阿尔伯塔投产。关键运行参数总结在表1中。最大持续速度(MCS)为11400rpm,入口压力1150 psi,出口压力3175 psi,18MW气体。轴承跨度Lb,与中轴直径Dms之比为13.2,表明轴非常的有弹性。nianxiangyuan
的横截面如图1所示。


不稳定性的严重程度可以在图2的轴心轨迹上看到。通过观察,五瓦块可倾瓦滑动轴承的轮廓线在6×9mils的峰-峰值轴心轨迹图中非常明显。图3中,突然出现的6.3mils的不稳定现象,显然是一种次同步振动,是由激发起的nianxiangyuan
一阶临界转速所致。


消除不稳定性的尝试包括轴承重新设计、油封修改、迷宫密封修改、平衡活塞修改、无叶扩散器改型、挤压油膜阻尼器改型,以及最后至少两个转子重新设计(图4)。第二转子重新设计包括增加中轴直径。最初,使用现有的叶轮锻件,切割和焊接叶轮轮毂,以增加叶轮内径以适应轴直径的增加(图5)。


显然,这种努力代价高昂。然而,它与Ekofisk不稳定性问题一起,提供了改进分析的可能,最终呈现出来现有的稳定性和迷宫密封型式以及新的API稳定性规范。
对数衰减率
稳定性分析和API稳定性验收准则的关键参数是对数衰减率。对数衰减率是自由振荡衰减率的量度,也是确定系统中存在的阻尼参数的简便方法。阻尼值越大,衰减率越快,系统的稳定性也越好。
对数衰减率被定义为任何两个连续振幅的比值的自然对数。参考图6,对数衰减率定义为:
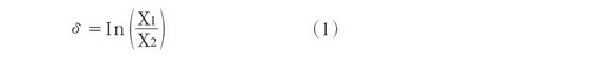
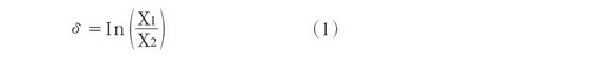

对于稳定的系统,具有正的衰减速率,对数衰减率为正。对于具有负衰减率的不稳定系统,对数衰减率为负。具有正对数衰减率的稳定系统包含足够的阻尼来克服初始激励。由此产生的位移将随着时间消散。相反,对数衰减率为负值的不稳定系统,没有足够的阻尼来克服初始激励,随着时间的推移将导致位移增加。
对数衰减率也可以用特征值的实部s和虚部ωd表达:
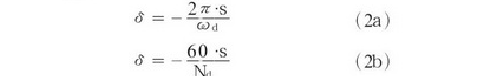
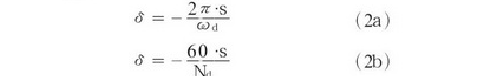
有阻尼固有频率可以有两种表达,或采用ωd,单位为rad/s,或采用Nd,单位为rpm。
例1: 12000HP,10级氢离心nianxiangyuan
第一个例子是一个10级12000马力氢离心nianxiangyuan
,具有65英寸的轴承跨度,Lb/Dms为11.3。转子重1340磅,在10750转/分的最大持续速度(MCS)下运行,干气密封和五瓦块可倾瓦滑动轴承如表1。
入口压力为800 psi,排气压力为1725 psi,气体摩尔质量为6。对数衰减率在零气动交叉耦合刚度下,在最小轴承间隙下Q为0.26,在最大轴承间隙下为0.40。从API规范617,第七版(2002),修正的Alford方程是:
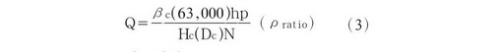
βc=3.0
hp=12,000 hp (total all stages)
Hc=Varies stage-to-stage
Dc=Varies stage-to-stage
N =10,750 rpm
ρratio=1.5 (total across compressor)
每级的Q均可由上述公式计算。由于每级的密度比和马力并不完全一致,因此每级马力被假定为上述总值的十分之一。每级密度比按上述总密度比假定,达到1/10的功率。叶轮出口宽度和叶轮直径是级间变量。所有10个Q值的总和是API Alford计算出来的,预期的交叉耦合值Qa为57250lbf/in。QA集中在转子中跨,得到的对数衰减率为:最小轴承间隙下为-0.4,最大轴承间隙下为-0.23。而API稳定性判定准则是对数衰减率大于0.1。因此,需要进行II级分析。
在进行分析之前,已经决定在平衡活塞上使用蜂窝密封。因此,上文中的稳定性结果包括蜂窝密封动态特性(Scharrer and Pelletti, 1994)。
以迷宫密封几何形状、级气体特性和级压力作为输入,对10个叶轮密封件中的每一个进行迷宫密封分析(Kirk,1990)。在密封入口处的气体涡流值被假定为0.6(对应于转速的60%)。保守起见,考虑密封件和密封套的加工公差范围,使用最小的密封间隙。10个迷宫密封总的Q为15700lbf/in。
忽略轴上密封作用,因为此处压降值很低。另外,密封流从静止部分进入密封,因此,入口涡流值低于密封涡流(图7)。高入口涡流将导致高Q值。

由于总的密封Q集中在转子中心,因此得到的对数衰减率,对应于最小轴承间隙为0.08,对应于最大轴承间隙为0.28。
除了估计迷宫密封处的入口涡流,还可以通过模拟叶轮表面和静止件之间的间隙来计算,如图8(Kirk,1990)。随着叶轮间隙模型的引入,入口涡流计算值为0.52,得到的Q值为7600 Lbf/in时的所有密封。由于总的密封Q集中在转子中心,所得对数衰减率值分别为:最小轴承间隙为0.17,最大轴承间隙为0.35。与I级分析一样,II级的API稳定性验收准则是大于0.1的对数衰减率。因此,该nianxiangyuan
在轴承间隙公差范围内满足API要求。

结果如表2所示,分别在图9和图10中给出了最小和最大轴承间隙。从图9和图10中也可以注意到零对数衰减率时的Q值,Q0。这些分别为22500和40000lbf/in的最小和最大轴承间隙。显然,使用改进的Alford力预测的稳定性水平较为保守。



密封入口涡流效应
入口涡流对总密封Q的影响如图11所示。在图12中给出了相应的稳定性影响。需要注意的是,在最小轴承和密封间隙下,入口涡流值为0.3时,对数衰减率将提高到提高0.28。(Childs and Ramsey, 1991;Moore and Hill, 2000)


密封间隙效应
密封间隙对Q的影响如图13所示。加工直径公差范围为16~20mils。假设由于叶轮的离心膨胀,最小直径密封间隙减小4mils,图13也给出了直径为12mils的最小工作间隙。图14中给出了入口涡流为0.6和最小轴承间隙时对稳定性的影响作用。


图15说明了收敛和发散型密封间隙对稳定性的影响。假设所有密封齿均为12mils的直径间隙,得到的对数衰减率为0.6。如果间隙从密封入口(直径为16mils)收敛到出口(直径为8mils),那么对数衰减率将减小到-0.11。反之,从入口(直径为8mils)到出口(直径为16mils),那么对数衰减率为0.23。这些计算值的前提条件是:假定最小轴承间隙,并且入口涡流值为0.6。

显然,应该优选发散型的间隙分布,以提高稳定性。对发散型间隙而言,虽然密封主刚度为负,这种影响是最小的。此外,对于发散型间隙情况,泄漏量实际上比恒定间隙减小了。对于这种nianxiangyuan
,从密封出口位置增加到密封入口位置,叶轮随转速的增大而变化,从而产生不同的密封间隙。
对于发散间隙,这种影响是最小的。此外,泄漏量实际上比恒定间隙减小了发散间隙情况。对于这种nianxiangyuan
,叶轮的增长速度从眼睛密封排放位置(叶轮眼)增加到眼睛密封入口位置,从而产生不同的密封间隙。
平衡活塞蜂窝密封
堵塞与入口涡流效应
蜂窝密封的一个问题是蜂窝孔可能堵塞或填充多余物。其它非迷宫式密封也可能存在堵塞,例如孔型密封件。
蜂窝密封的这种堵塞孔效应如图16所示,图中给出了最小轴承间隙,以及三个不同的蜂窝密封入口涡流值:0.8,一个较糟糕的值;0.6,一个更现实的值;和0.3,模拟包含涡流制动器。结果表明,随着蜂窝孔的填充或堵塞,稳定性降低。对于入口涡流为0.6的情况,只要有小于48%的孔隙填充,则对数衰减率就会大于0.1,满足API要求。对于包含涡流制动器(入口涡流为0.3),只要孔隙填充数少于60%,对数衰减率就大于0.1。

例2:65000 马力,3级丙烷制冷nianxiangyuan
第二个例子是用于制冷的三级、三段65000 马力丙烷nianxiangyuan
,其具有230inch的轴承跨度和Lb/Dms=10.3。转子的重量超过36000磅,工作转速3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为20 psi,出口压力为100 psi,气体摩尔重量为44。大型制冷nianxiangyuan
的典型特征是具有较低的对数衰减率和相对较小的不稳定力表现。这台机器也不例外。该nianxiangyuan
的基本对数衰减率(仅就转子和轴承而言,Q=0)在轴承公差范围内分布于0.18到0.13不等。
过去对具有多过程段的nianxiangyuan
,在考虑“Wachel”型方程(Wachel和Von Nimz,1981)时,出现了适用性问题。在大多数情况下,通过逐级应用修正的Alford方程,已经解决了这些问题。在该应用中,每级表示一个过程段,该过程段内将侧流添加到主流中,这发生在第二叶轮和第三叶轮之前。图17给出了nianxiangyuan
的转子动力学模型。


应用公式(3),可以计算预期的不稳定力Qa,总预期的失稳力Qa为23046 lbf/in。将这应用于转子中心,分别得到最小和最大轴承刚度的对数衰减率为0.15和0.09。图18显示了稳定性灵敏度曲线。(轴承间隙和油入口温度的公差范围限定了轴承刚度的范围)。根据API的要求,由于最坏情况δa<0.1,用Kirk(1990)开发的方法进行二级分析,以预测叶轮迷宫式密封件的性能。这些不稳定力被施加在密封的实际位置上。对于相同范围内的轴承刚度,对数衰减率是针对以下条件计算的:
仅转子和轴承
转子、轴承和叶轮迷宫密封
转子、轴承、叶轮迷宫密封和平衡活塞
表3包含了二级分析的结果和使用修正的Alford力对转子稳定性的估计。正如预期的那样,由于迷宫密封(包括平衡活塞)的激励力很小,因此对转子稳定性影响较小。对于这个应用,使用改进的Alford力预测的稳定性水平是保守的。

例3 30000马力4级喷射nianxiangyuan
(略)
第四个例子是11000马力的四级离心nianxiangyuan
,用于喷射,具有48英寸的轴承跨度,Lb/Dms=7.26。转子重422磅,运行转速为9900rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为5600 psi,出口压力为9000 psi。
就喷射方面而言,该nianxiangyuan
被认为具有较高的排放压力范围和中等的功率与重量比值。在这样的情况下,由于nianxiangyuan
中气体的密度升高,不稳定力预计会更高。实际上,由于平均气体密度为115 kg/m3,需要进行II级分析。如前所述,制造商保守地设计了具有较大中心轴段的nianxiangyuan
,以抵消预期的更高的不稳定力(图19)。

这种情况下,修改后的Alford力计算值为72854lbf/in,大致等于示例3中的nianxiangyuan
。(图20)。较高的气体密度抵消了前面例子中较高的马力。因此,对于这两个例子,预期的不稳定力水平大致相同。表3包含了I级和II级分析的稳定性分析结果。与其它喷射nianxiangyuan
一样,由于Q0<2Qa,需要进行II级分析,这表明预期的失稳力和驱动系统不稳定所需的量之间存在足够的安全余量。

如前所述,对于两个喷射nianxiangyuan
来说,Alford不稳定力几乎相等。表3通过比较两个II级分析,证实了这一事实。从基础值到包括所有不稳定力条件,在轴承系数变化范围内,对于第一喷射nianxiangyuan
的对数衰减率大约为-0.55和-0.40,对于第二喷射nianxiangyuan
的对数衰减率约为-0.45和-0.30。考虑到转子和轴承几何形状的差异,这两者可视为相当或一致。与前面的例子不同,平衡活塞产生了大部分的不稳定力。
由于nianxiangyuan
内气体平均密度上升,因此需要进行II级分析。这台nianxiangyuan
成功地通过了满负荷试验,没有发生稳定性问题。
例5 混合制冷
在前三个例子中,通过比较I级和II级分析,得到了对数衰减率值,来确定修正的Alford方程的保守性。在本节中,提出了一种比较等效集中不稳定力的更直接的方法,类似于Memmott (2000)。示例3中,喷射nianxiangyuan
与较大的制冷nianxiangyuan
一起使用。93000马力的混合制冷nianxiangyuan
(例5)具有222英寸的轴承跨度,Lb/Dms为10.2。图21比较了这两种nianxiangyuan
。转子重44730磅,运行转速为3000rpm,采用干气密封和五瓦块可倾瓦滑动轴承(表1)。入口压力为60 psi,使用25MW的气体,具有320 psi的出口压力。

为了产生与修正的Alford方程计算等效的失稳力,使用以下关系计算每个密封件的等效交叉耦合刚度:


K和C值由迷宫密封分析(Kirk, 1990)确定,转子中心的等效模态交叉耦合定义为:


从第一阻尼固有频率的归一化模态振型确定模态影响因子Mf,表征密封位置处的位移。对所有密封位置进行求和,得到交叉耦合力。这种模态交叉耦合,Qm,连同II级分析中计算的对数衰减率值一起,在最大轴承刚度的条件下,绘制在两个nianxiangyuan
实例的稳定性灵敏度图上。
图22为例子3种第一种喷射nianxiangyuan
的结果。


该nianxiangyuan
的最小模态系数仅为0.91,反映了nianxiangyuan
的轴具有较好的刚性工作条件(stiffer shaft operation)。考虑到迷宫密封和平衡活塞力,计算模态交叉耦合系数为44933lbf/in。表3中,包括所有不稳定力的II级对数衰减率,在最大支承刚度时,为0.48。在灵敏度图上绘制这一点,人们发现该点几乎直接位于通过在转子中心放置不同量值的交叉耦合刚度而得到的直线上。需要强调的是,对数衰减率绘制的δm是由II级分析计算得到的,考虑位于实际位置的密封效应。从这一点可以得出如下结论:
modal reduction产生的交叉耦合力直接与修正Alford力相媲美。
模态交叉耦合还提供了基于实际密封系数的转子裕度指示。(在这种情况下,将44933 lbf/in与95300lbf/in的Q0量进行比较。大约存在两倍安全余量,或更简单地说,迷宫密封的不稳定效应可能比预测不稳定条件之前的计算值大两倍。
对混合制冷nianxiangyuan
进行重复计算(例5)。对于这种nianxiangyuan
,最小模态系数为0.56,表示轴具有更灵活的弯曲模态。在II级分析中包括两种密封结构,一种具有分流的平衡活塞另一种是没有分流的密封。模态交叉耦合和最终II级对数衰减率值绘制如图23所示。与喷射nianxiangyuan
一样,这两个点与I级分析的灵敏度线密切相关。这是真实的情况,即使在分流平衡活塞的情况下,净交叉耦合项为负(或稳定)。
结论
开展了API水平I级修正的Alford交叉耦合力的计算,并证实了nianxiangyuan
的不稳定力是一种保守估计。研究了几个工业领域的应用,包括氢nianxiangyuan
、两个高压喷射nianxiangyuan
、一个具有高功率与重量比的nianxiangyuan
,以及两个大型制冷nianxiangyuan
,包括多级结构。在所有情况下,修正的Alford力,将产生最差的稳定性水平。
此外,检查了II级分析的细节,以确定哪些参数是确定离心nianxiangyuan
稳定性的关键。一些已知的影响,包括轴承间隙公差和迷宫密封入口涡流,显示出对10级氢气nianxiangyuan
的稳定性水平有重大影响。在恒定的入口涡流为0.6的情况下,仅仅将在叶轮密封处的齿隙倾斜从8 mils 径向收敛区变为8 mils径向发散区,预测的对数衰减率将从-0.11变为0.23。这为提高离心式离心nianxiangyuan
的稳定性提供了另一个简单的途径。
最后,提出了一种模态方法来直接比较I级和II级不稳定力。除了确认修正的Alford力的保守性外,模态方法还允许使用稳定性灵敏度曲线来逼近迷宫密封系数相对于零对数衰减率阈值的安全裕度。
参数如下:
Cs=Seal diametral clearance (mils)
C=Principle damping (lbf-sec/in)
Dc=Impeller diameter (inch)
Dms=Midshaft diameter (inch)
Hc=Minimum width of the impeller or discharge volute (inch)
hp=Horsepower (hp)
k=Cross-coupled stiffness (lbf/in)
Lb=Bearing span, (inch)
Mf=Modal influence factor
N=Speed (rpm)
Nd=Damped natural frequency (cpm)
Pdisch=Discharge pressure (psi)
Pin=Inlet pressure (psi)
Q=Aerodynamic cross-coupling (lbf/in)
Qa=Anticipated aerodynamic cross-coupling (lbf/in)
Qeq=Equivalent cross-coupling (lbf/in)
Qm=Modal cross-coupling (lbf/in)
Q0=Aerodynamic cross-coupling for zero log dec (lbf/in)
s=Real part of eigenvalue
X1,2=Amplitude (mils)
β=Efficiency factor δ = Log dec
δa=Log dec for Qa
δm=Final log dec from the Level II analysis
ρratio=Density ratio
ωd=Damped natural frequency (rad/sec)
ωcs=Damped first natural frequency (rad/sec)




网友评论
条评论
最新评论